EQUATION OF PARABOLA

Equation of a Parabola in Standard form

Vertex at Origin : 

y²  =  4ax (opens right, a > 0)

y²  =  -4ax (opens right, a > 0)

x²  =  4ay (opens up, a > 0)

x²  =  -4ay (opens down, a > 0)

Vertex at (h, k) : 

(y - k)²  =  4a(x - h) (opens right, a > 0)

(y - k)²  =  -4a(x - h) (opens right, a > 0)

(x - h)²  =  4a(y - k) (opens up, a > 0)

(x - h)²  =  -4a(y - k) (opens down, a > 0)

Equation of a Parabola in Vertex form

Vertex at Origin : 

y  =  ax² (opens up, a > 0)

y  =  -ax² (opens down, a > 0)

x  =  ay² (opens right, a > 0)

x  =  -ay² (opens left, a > 0)

Vertex at (h, k) : 

y  =  a(x - h)² + k (opens up, a > 0)

y  =  -a(x - h)² + k (opens down, a > 0)

x  =  a(y - k)² + h (opens right, a > 0)

y  =  -a(y - k)² + h (opens left, a > 0)

Equation of a Parabola in Intercept form

y  =  a(x - p)(x - q)  (opens up, a > 0)

y  =  -a(x - p)(x - q)  (opens down, a > 0)

x  =  a(y - p)(y - q)  (opens right, a > 0)

x  =  -a(y - p)(y - q)  (opens left, a > 0)

Equation of a Parabola in General form

y  =  ax² + bx + c (opens up, a > 0)

y  =  -ax² + bx + c (opens down, a > 0)

x  =  ay² + by + c (opens right, a > 0)

x  =  -ay² + by + c (opens left, a > 0)

Solved Problems

Problem 1 : 

Find the standard form equation of the parabola that has vertex at origin and focus at (0, 1).

Solution : 

Plot the vertex (0, 0) and focus (0, 1) on the xy-plane. 

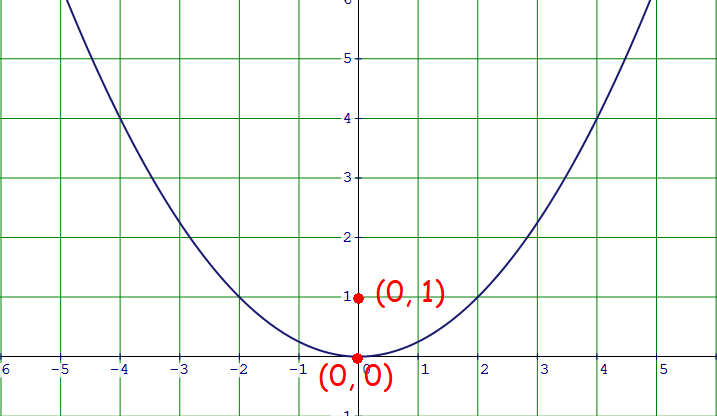
The parabola is open up with vertex at origin. 

Standard form equation of a parabola that opens up with vertex at origin :

x²  =  4ay

Distance between the vertex and focus is 1 unit. 

That is, a = 1. 

x²  =  4(1)y

x²  =  4y

Problem 2 : 

Find the standard form equation of the parabola that has vertex at (2, -1) and focus at (-1, -1).

Solution : 

Plot the vertex (0, 0) and focus (0, 1) on the xy-plane. 

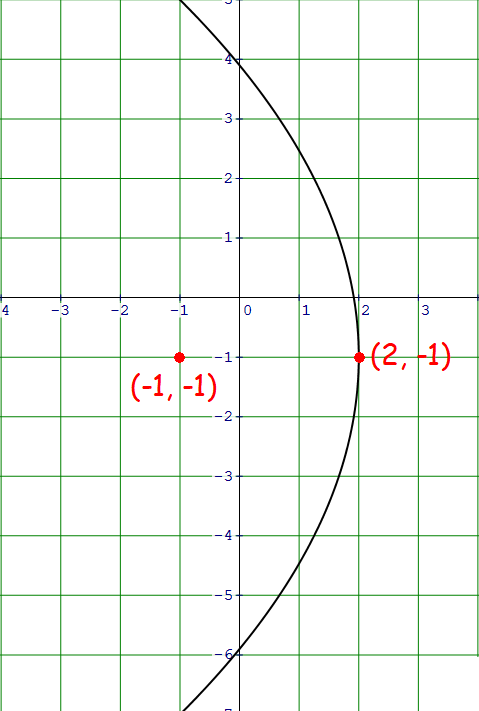
The parabola is open to the left with vertex at (2, -1).

Standard equation of a parabola that opens left with vertex at (h, k) : 

(y - k)²  =  -4a(x - h)

Vertex (h, k) = (2, -1).

(y + 1)²  =  -4a(x - 2)

Distance between the vertex and focus is 3 units. 

That is, a = 3. 

(y + 1)²  =  -4(3)(x - 2)

(y + 1)²  =  -12(x - 2)

Problem 3 : 

Find the vertex form equation of the parabola :

Opens left or right, Vertex (0,0), Passes through (-16, 2)

Solution : 

Vertex form equation of a parabola that opens left or right with vertex at origin : 

x  =  ay²

It passes through (-16, 2). Substitute (x, y) = (-16, 2). 

-16  =  a(2)²

-16  =  a(4)

Divide each side by 4.

-4  =  a

Vertex form equation of the parabola : 

x  =  -4y²

Problem 4 :

Find the vertex form equation of the parabola :

Opens left or right, Vertex (-1, -2), Passes through (11, 0)

Solution : 

Vertex form equation of a parabola that opens left or right with vertex at (h, k) : 

x  =  a(y - k)² + h

Vertex (h, k) = (-1, -2).

x  =  a(y + 2)² - 1

It passes through (11, 0). Substitute (x, y) = (11, 0). 

11  =  a(0 + 2)² - 1

11  =  a(2)² - 1

11  =  4a - 1

Add 1 to each side. 

12  =  4a

Divide each side by 4.

3  =  a

Vertex form equation of the parabola :

x  =  3(y + 2)² - 1

Problem 5 : 

Write the intercept form equation of the parabola shown below.

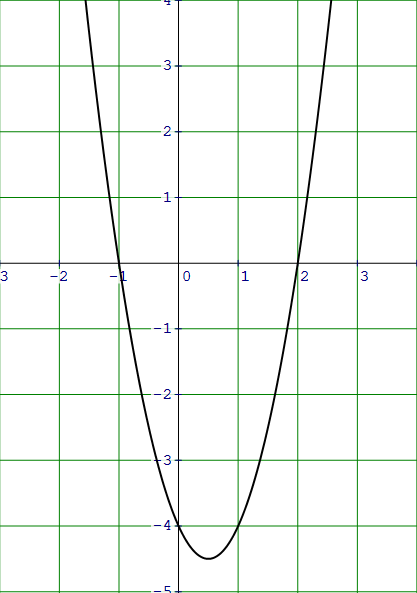
Solution : 

Intercept form equation of the above parabola :

y  =  a(x - p)(x - q)

Because x-intercepts are (-1, 0) and (2, 0), 

x  =  -1 -----> x + 1  =  0

x  =  2 -----> x - 2  =  0

Then, 

y  =  a(x + 1)(x - 2)

It passes through (0, -4). Substitute (x, y) = (0, -4). 

-4  =  a(0 + 1)(0 - 2)

-4  =  a(1)(-2)

-4  =  -2a

Divide each side by -2.

2  =  a

Intercept form equation of the parabola :

y  =  2(x + 1)(x - 2)

Problem 6 : 

Find the equation of the parabola in general form :

Opens up or down, Vertex (3, 1), Passes through (1, 9)

Solution : 

First, find the equation of the parabola in vertex form, then convert it to general form. 

Vertex form equation of a parabola that opens up or down with vertex at (h, k) :

y  =  a(x - h)² + k

Vertex (h, k) = (3, 1).

y  =  a(x - 3)² + 1

It passes through (1, 9). Substitute (x, y) = (1, 9). 

9  =  a(1 - 3)² + 1

9  =  a(-2)² + 1

9  =  4a + 1

Subtract 1 from each side. 

8  =  4a

Divide each side by 4.

2  =  a

Vertex form equation of the parabola : 

y  =  2(x - 3)² + 1

Convert the above vertex form equation to general form. 

y  =  2[x² - 2(x)(3) + 3²] + 1

y  =  2(x² - 6x + 9) + 1

Distribute. 

y  =  2x² - 12x + 18 + 1

y  =  2x² - 12x + 19

Problem 7 : 

Write the following general form equation of the parabola in vertex form.

y  =  3x² - 18x + 29

Solution : 

y  =  3x² - 18x + 29

y  =  3(x² - 6x) + 29

y  =  3[x² - 2(x)(3) + 3² - 3²]  + 29

y  =  3[(x - 3)² - 9]  + 29

y  =  3(x - 3)² - 27 + 29

y  =  3(x - 3)² + 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.