ALGEBRAIC REPRESENTATIONS OF TRANSFORMATIONS WORKSHEET
Problem 1 :
Trapezoid ABCD has the vertices A (1, 0), B(4, 0), C(4, -4) and D(0, -4). Graph the trapezoid ABCD and its image after a translation of 5 units to the left and 3 units up.
Problem 2 :
A pentagon has the vertices A(-5, 6), B(-3, 6), C(-2, 4), D(-3, 1) and E(-5,1). Find the vertices of rectangle A'B'C'D'E' after a reflection across the y-axis. Then graph the pentagon and its image.
Problem 3 :
The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 90° counterclockwise about the origin.
Problem 4 :
A quadrilateral has the following vertices A(0, 0), B(1, 2), C(4, 2) and D(3, 0). Rotate the quadrilateral 180° clockwise about the origin.

1. Answer :
Step 1 :
Let A', B', C' and D' be the vertices of the translated figure.
Since there is a translation of 5 units to the left and 3 units up, we have to subtract 5 from x-coordinate and add 3 to y-coordinate of each vertex.
A' ------> (1-5, 0+3) = (-4, 3)
B' ------> (4-5, 0+3) = (-1, 3)
C' ------> (4-5, -4+3) = (-1, -1)
D' ------> (0-5, -4+3) = (-5, -1)
Step 2 :
Sketch the trapezoid ABCD and its image A'B'C'D'.
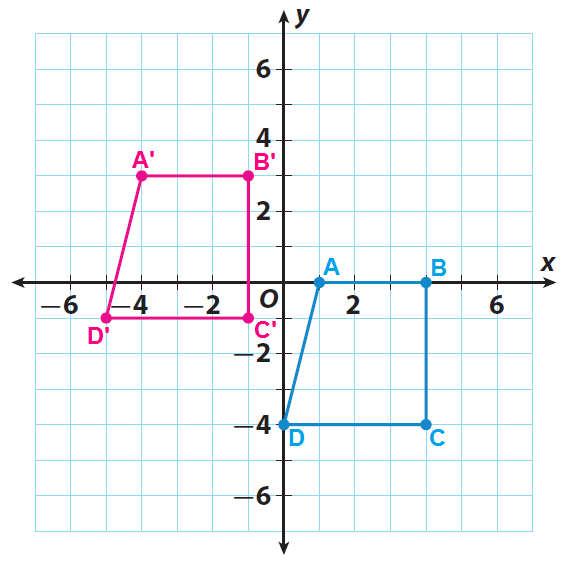
2. Answer :
Step 1 :
Apply the rule to find the vertices of the image.
Since there is a reflection across the y-axis, we have to multiply each x-coordinate by -1.
That is, (x, y) ----> (-x, y).
Step 2 :
A(-5, 6) ----> A'(5, 6)
B(-3, 6) ----> B'(3, 6)
C(-2, 4) ----> C'(2, 4)
D(-3, 1) ----> D'(3, 1)
E(-5, 1) ----> E'(5, 1)
Step 3 :
Graph the pentagon ABCDE and its image.
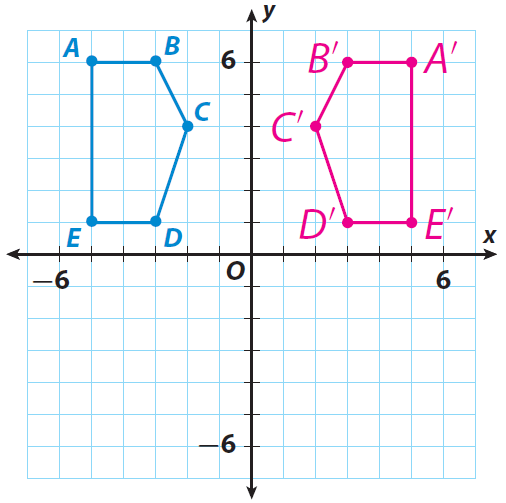
3. Answer :
Step 1 :
Trace triangle XYZ and the x- and y-axes onto a piece of paper.
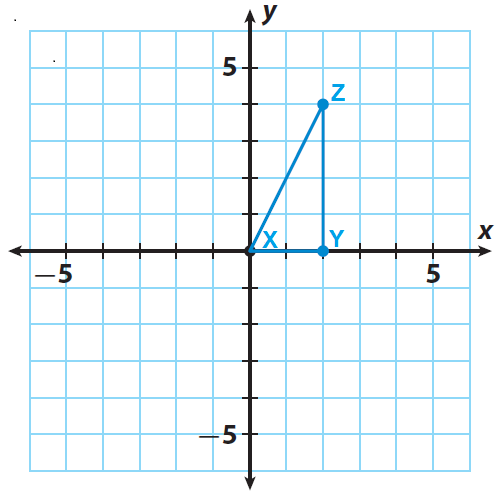
Step 2 :
Let X', Y' and Z' be the vertices of the rotated figure.
Since the triangle is rotated 90° counterclockwise about the origin, the rule is
(x, y) ------> (-y, x)
Step 3 :
X(0, 0) ------> X'(0, 0)
Y(2, 0) ------> Y'(0, 2)
Z(2, 4) ------> Z'(-4, 2)
Step 4 :
Sketch the image X'Y'Z' using the points X'(0, 0), Y'(0, 2) and Z'(-4, 2).
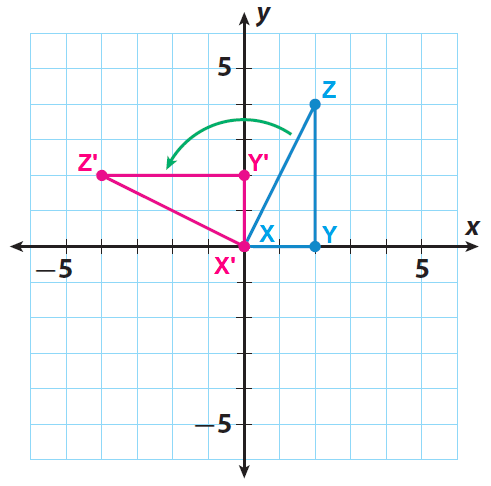
4. Answer :
Step 1 :
Trace the quadrilateral ABCD and the x- and y-axes onto a piece of paper.
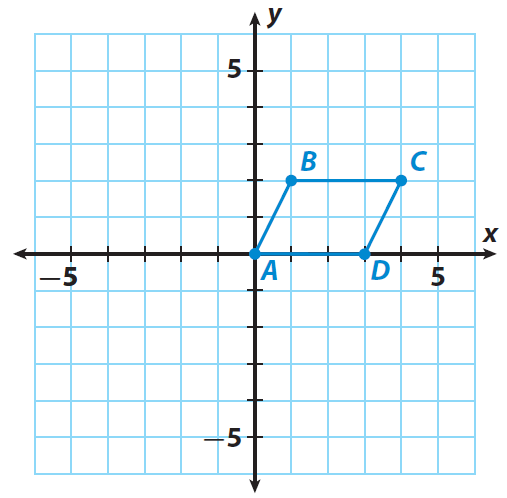
Step 2 :
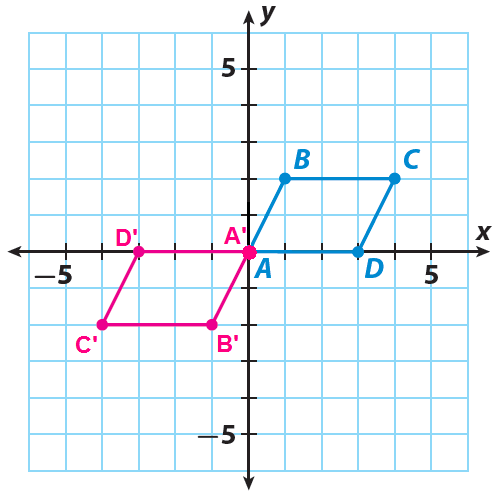
Let A', B', C' and D' be the vertices of the rotated figure.
Since the quadrilateral is rotated 180° clockwise about the origin, the rule is
(x, y) ------> (-x, -y)
Step 3 :
A(0, 0) ------> A'(0, 0)
B(1, 2) ------> B'(-1, -2)
C(4, 2) ------> C'(-4, -2)
D(3, 0) ------> D'(-3, 0)
Step 4 :
Sketch the image A'B'C'D' using the points A'(0, 0), B'(-1, -2), C(-4, -2) and D'(-3, 0).
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Given Composite Function : How to Find the Inside or Outside Function
Jan 22, 25 02:43 AM
How to Find the Inside or Outside Function From the Given Composite Function -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Jan 20, 25 09:31 PM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 101)
Jan 20, 25 09:27 PM
Digital SAT Math Problems and Solutions (Part - 101)
