AREA AND PERIMETER OF SIMILAR FIGURES

Two figures that have the same shape are said to be similar. When two figures are similar, lengths of their corresponding sides will be in proportional. To determine, if the rectangles below are similar, compare their corresponding sides.

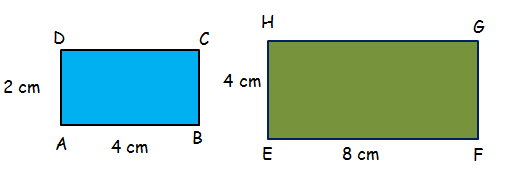
AB : EF  =  AD : EH

4 : 8  =  2 : 4

1 : 2  =  1 : 2

The lengths of their corresponding sides are proportional. So, the above two rectangles are similar. 

Perimeter :

If two similar figures have a scale factor of a : b, then the ratio of their perimeters is a : b.

Area :

If two similar figures have a scale factor of a : b, then the ratio of their areas is a² : b².

Note : 

1. If the perimeters of two similar figures are in the ratio

a : b,

then their areas will be in the ratio

a² : b²

2. If the areas of two similar figures are in the ratio 

a : b,

then their perimeters will be in the ratio

√a : √b

Example 1 :

The two rectangles given below are similar. Find the perimeter of the rectangle EFGH.

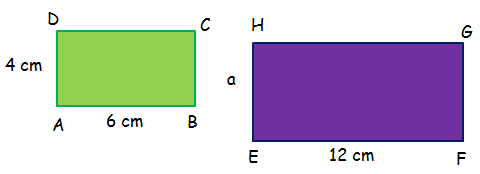
Solution :

Because the above rectangles ABCD and EFGH are similar, the lengths of the corresponding sides will be proportional.

AB/EF  =  AD/EH

6/12  =  4/a

1/2  =  4/a

2/1  =  a/4

Multiply each side by 12. 

(2/3) ⋅ 12  =  a

8  =  a

Perimeter of rectangle EFGH is  

=  2(l + w)

=  2(12 + 8)

=  2(20)

=  40

So, the perimeter of the rectangle EFGH is 40 cm. 

Example 2 :

The two parallelograms shown below are similar. Find the perimeter of the parallelogram ABCD. 

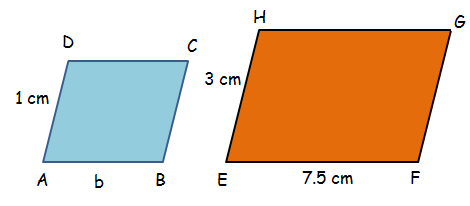
Solution :

Because the above parallelograms ABCD and EFGH are similar, the lengths of the corresponding sides will be proportional.

AB/EF  =  AD/EH

b/1  =  7.5/3

b  =  2.5

Perimeter of the parallelogram ABCD is  

=  2(2.5 + 1)

=  2(3.5)

=  7

So, the perimeter of the parallelogram ABCD is 7 cm. 

Example 3 :

The perimeters of two similar triangles is in the ratio 3 : 4. The sum of their areas is 75 cm². Find the area of each triangle.

Solution :

Given :  Perimeters of two similar triangles is in the ratio

3 : 4

Then,

Perimeter of the 1^st Δ  =  3x

Perimeter of the 2^nd Δ  =  4x

And also, 

Area of 1^st Δ : Area 2^nd Δ  =  (3x)² : (4x)²

Area of 1^st Δ : Area 2^nd Δ  =  9x² : 16x²

Given : Sum of the areas is 75 cm².

Then, 

9x² + 16x²  =  75

25x²  =  75

Divide by 25 from each side. 

25x²  =  75

x²  =  3

Area of 1^st Δ  =  9(3)  =  27 cm²

Area of 2^nd Δ  =  16(3)  =  48 cm²

Example 4 :

The areas of two similar triangles are 45 cm² and 80 cm². The sum of their perimeters is 35 cm. Find the perimeter of each triangle. 

Solution :

Ratio between the areas of two triangles is

=  45 : 80

=  9 : 16

Then, the ratio between the perimeters of two triangles is

=  √9 : √16

=  3 : 4

So,

Perimeter of 1^st Δ  =  3x

Perimeter of 2^nd Δ  =  4x

Given : Sum of the perimeters is 35 cm.

Then,

3x + 4x  =  35

7x  =  35

x  =  5

Therefore, 

Perimeter of 1^st Δ  =  3x  =  3(5)  =  15 cm

Perimeter of 2^nd Δ  =  4x  =  4(5)  =  20 cm

Example 5 :

Cube B is an enlargement of cube A.

(a) What is the scale factor of enlargement?

(b) How many times larger is the surface area of B than A?

(c) How many times larger is the volume of cube B than A?

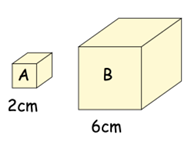
Solution :

Side length of cube a = 2 cm

Side length of cube b = 6 cm

Ratio between corresponding side = 2 : 6

= 1 : 3

(a) So, the scale factor is 1 : 3

(b) When corresponding sides are in the ratio a : b, its surface area will be a² : b²

Surface area of small cube : Surface area of large cube

= 1 : 9

Surface area of cube B is 9 times of surface area of cube A.

(c) When corresponding sides are in the ratio a : b, its surface area will be a³ : b³

Volume of small cube : Volume of large cube

= 1³ : 3³

= 1 : 27

Example 6 :

The surface areas of two similar shapes are in the ratio 25 : 81. The length of the smaller shape is 30 cm. Work out the length of the larger shape.

Solution :

Ratio of surface area of similar shapes = 25 : 81

Let side lengths of shapes be a and b.

a² : b² = 25 : 81

a² : b² = 5² : 9²

Corresponding sides are 5 and 9 respectively.

Side length of small shape = 5(6) ==> 30 cm

Side length of large shape = 9(6) ==> 54 cm

Example 7 :

The volumes of two similar shapes are in the ratio 1000 : 27. The surface area of the larger shape is 250 cm² Work out the surface area of the smaller shape.

Solution :

Ratio between volume of two shapes = 1000 : 27

= 10³ : 3³

Ratio between corresponding sides be a : b, that is 10 : 3.

Surface area of larger shape : Surface area of smaller shape

= a² : b²

250 : Surface area of smaller shape = 10² : 3²

250 / Surface area of smaller shape = 100 / 9

250(9) = 100(surface area of smaller shape)

Surface area of smaller shape = 250(9)/100

= 22.5 cm²

So, the required surface area of smaller shape is 22.5 cm².

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.