CHARACTERISTICS OF QUADRATIC FUNCTIONS

If you draw the graph for a quadratic equation, you can get the shape parabola. 

Each quadratic functions will have some characteristics. 

They are 

• Axis of symmetry
• x and y-intercepts
• Zeroes
• vertex
• Point symmetric to y-intercept

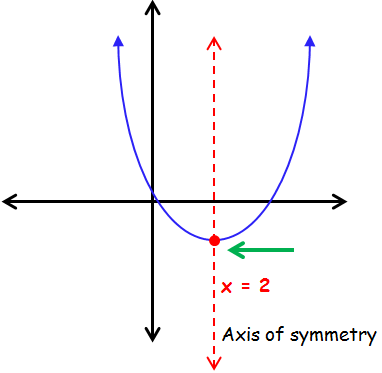
Axis of Symmetry :

The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves. The axis of symmetry always passes through the vertex of the parabola . The x -coordinate of the vertex is the equation of the axis of symmetry of the parabola.

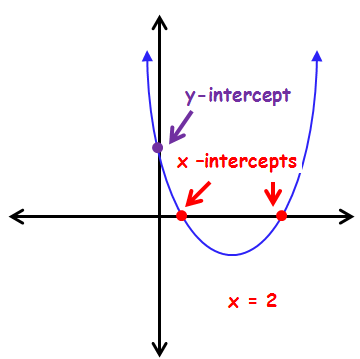
X and Y Intercepts :

The point at which the parabola cuts the x-axis is known as x-intercept.To find x-intercept we have to put y = 0.

The point at which the parabola cuts the y-axis is known as y-intercept.To find y-intercept we have to put x = 0.

Zeroes :

We can get the zeroes of a quadratic function by applying y = 0. Zeroes of a quadratic function and x-intercepts are same.

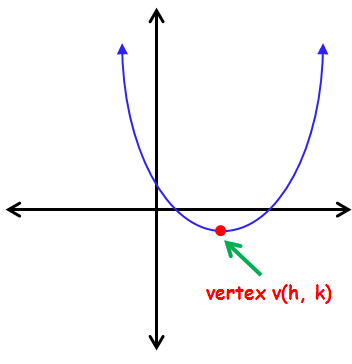
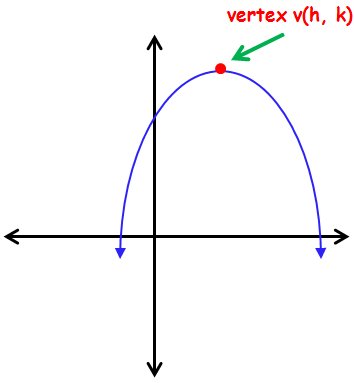
Vertex :

The vertex of a parabola is the point where the parabola crosses its axis of symmetry.

The vertex of the parabola is the highest or lowest point also known as maximum value or minimum value of the parabola.

Point Symmetric to Y-Intercept :

The y-intercept (and other points) can be reflected across the axis of symmetry to find other points on the graph of the function.

The points  which are having same horizontal distance from the axis is known as symmetric points.

Symmetric points is also known as mirror point.

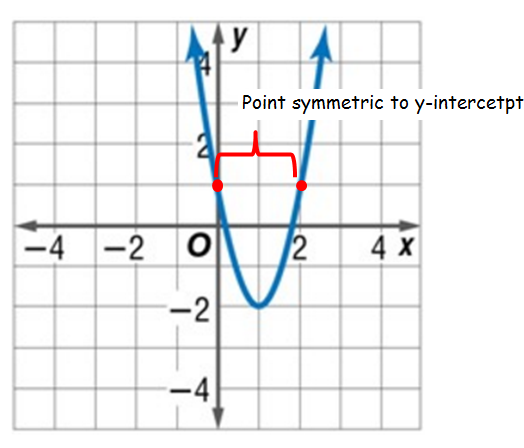
Example :

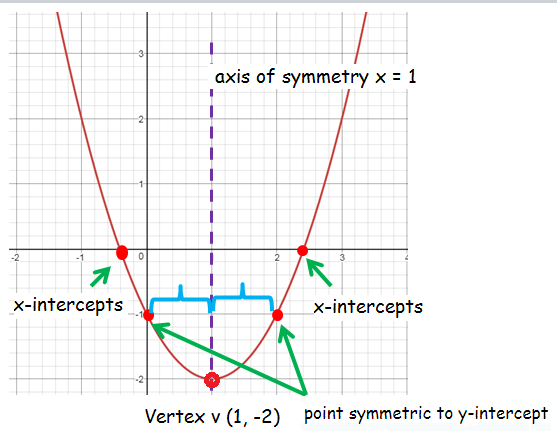
Find the equation of axis of symmetry, x and y intercepts, zeroes, vertex and point symmetric to y-intercept. Sketch the graph of the function.

y  =  x² - 2 x - 1

Solution :

Comparing

y  =  x² - 2 x - 1

and

y  =  ax² + bx + c,

we get

a  =  1, b  =  -2 and c  =  -1

The given parabola is symmetric about y axis.

Because a > 0, the parabola is open upward.

Equation of Axis :

x  =  -b/2a

x  =  -(-2)/2(-1)

x  =  (-2) / (-2)

x  =  1

X and Y Intercepts :

Zeroes :

Let p(x)  =  x² - 2 x - 1. 

If p(x)  =  0, then

x² - 2 x - 1  =  0

Solving the above quadratic equation using quadratic formula, we get

x  =  (2  ± √8)/2

x  =  1 ± √2

x  =  1 + √2, x = 1 - √2

x  =  2.414, -0.414

Vertex :

Formula to find x-coordinate of the vertex is

x  =  -b/2a

x  =  -(-2) / 2(1)

x  =  2/2

x  =  1

Substitute x = 1 in the given equation function.

y  =  1² - 2(1) - 1

y  =  1 - 3

y  =  -2

Vertex of the parabola is (1, -2)

Point Symmetric to Y-Intercept :

The point symmetric to y intercept will have the same horizontal distance from the axis of symmetry.

To find that point we have to substitute y-intercept into the given function. 

-1  =  x² - 2 x - 1

Add 1 to each side. 

0  =  x² - 2x

0  =  x(x - 2)

x  =  0 and x  =  2

So, points symmetric to y-intercept are

(0, -1) and (2, -1)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.