COMPLEX PLANE

The complex plane, also known as the Argand plane, is a fundamental concept in complex analysis and provides a geometric representation of complex numbers. In the complex plane, each complex number is represented as a point with coordinates based on its real and imaginary parts.

A complex number z = x + iy is uniquely determined by an ordered pair of real numbers (x, y).

The numbers 2 -7i, 5, and -3i can be equated to the points as shown below.

2 - 7i = (2, -7)

5 = (9, 0)

-3i = (0, -3)

In this way, we can associate a complex number  z = x + iy with a point (x, y) in a coordinate plane.

If we consider horizontal axis or x-axis as real axis and vertical axis or y-axis as imaginary axis to represent a complex number, then the xy-plane is called complex plane or Argand plane, which is named after the Swiss mathematician Jean Argand (1768 – 1822).

A complex number is represented not only by a point, but also by a position vector pointing from the origin to the point. The number, the point, and the vector will all be denoted by the same letter z . As usual we identify all vectors which can be obtained from each other by parallel displacements.

In real analysis, C denotes the set of all complex numbers. Geometrically, a complex number can be viewed as either a point in R² or a vector in the Argand plane.

Complex number as a point :

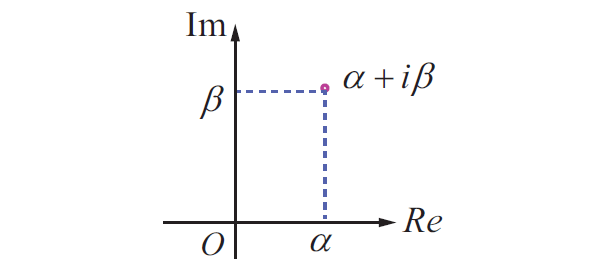
Complex number by a position vector pointing from the origin to the point :

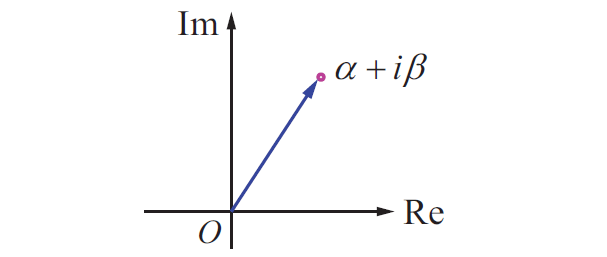
Complex number as a vector :

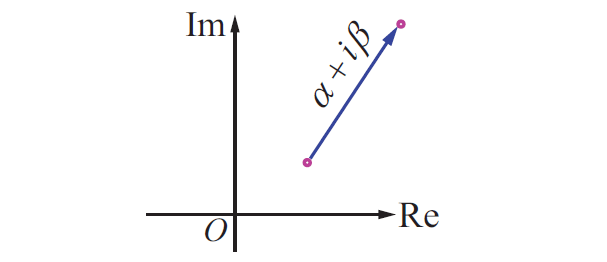
Here are some complex numbers :

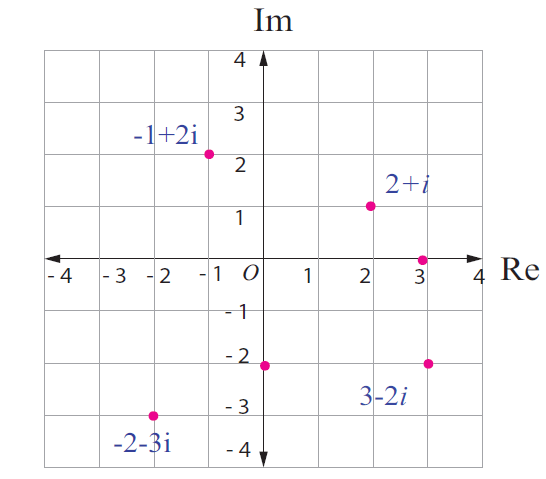
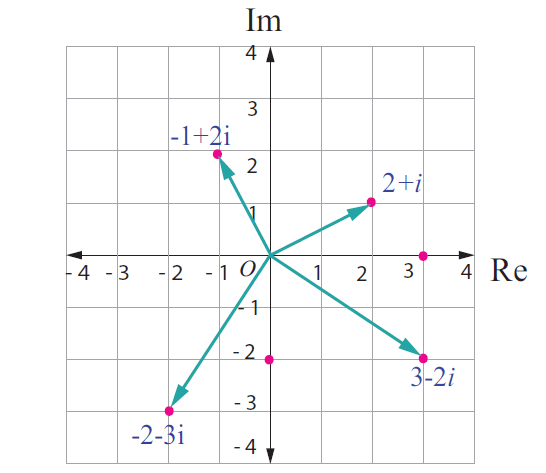
2 + i

-1 + 2i

3 - 2i

0 - 2i

-2 - 3i

3 + 0i

Some of them are plotted in Argand plane as points and as vectors.

Complex numbers as points :

Complex numbers as vectors :

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.