CONSTRUCTION OF MEDIAN  OF A TRIANGLE

In this section, you will learn how to construct median of a triangle. 

Before we learn how to consstruct circumcenter of a triangle, first we have to learn how to construct perprendicular bisector. 

So, let us learn how to construct perpendicular bisector. 

Construction of Perpendicular Bisector - Steps

To construct a perpendicular bisector, we must need the following instruments.

1. Ruler

2. Compass

The steps for the construction of a perpendicular bisector of a line segment are :

Step 1 :

Draw the line segment AB. 

Step 2 :

With the two end points A and B of the line segment as centers and more than half the length of the line segment as radius draw arcs to intersect on both sides of the line segment at C and D.

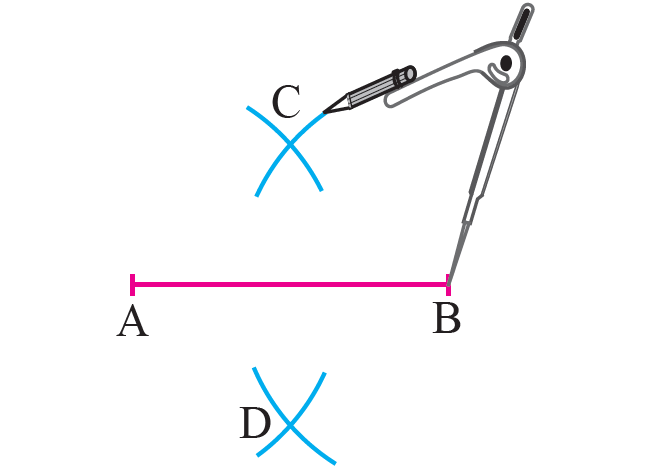
Step 3 :

Join C and D to get the perpendicular bisector of the given line segment AB.

In the above figure, CD is the perpendicular bisector of the line segment AB.

This construction clearly shows how to draw the perpendicular bisector of a given line segment with compass and straightedge or ruler.

This bisects the line segment (That is, dividing it into two equal parts) and also perpendicular to it. 

Now, let us see how to construct median of a triangle. 

Constructing Median of a Triangle

To construct median of a triangle, we must need the following instruments.

1. Ruler

2. Compass

Let us see, how to construct median of a triangle through the following example.  

Construct median to the side BC of the triangle ABC with AB = 6 cm, BC = 7 cm and AC = 5 cm.

Step 1 :

Draw triangle ABC using the given measurements. 

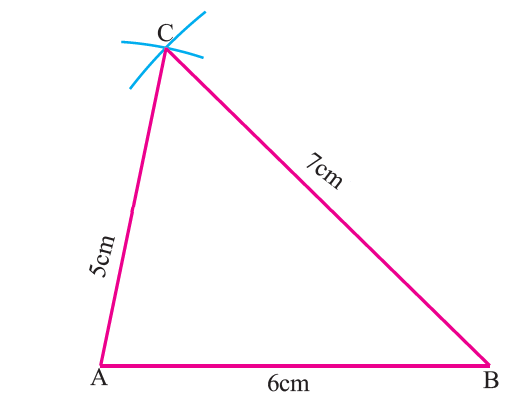
Step 2 :

Construct the perpendicular bisector of the side BC to find midpoint E of BC. 

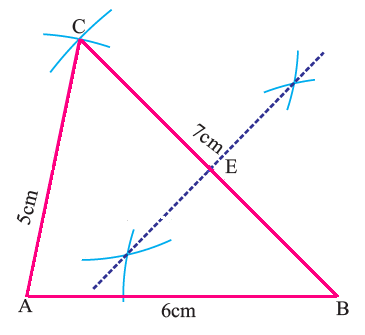
Step 3 :

Now, join the vertex A and the mid point E of BC. 

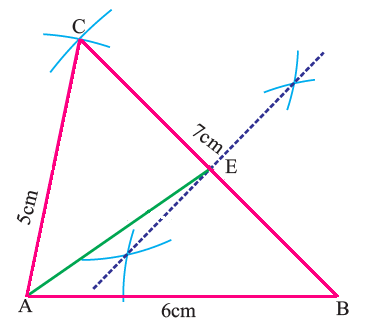
Now, AE is the median to the side BC of the triangle ABC. 

This construction clearly shows how to draw median of a triangle with compass and straightedge or ruler. The median divides the side into two equal halves. 

In the above example, median AE divides the side BC  in to two equal halves. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.