DECIMAL REPRESENTATION OF RATIONAL NUMBERS
Let us consider the rational number p/q, where both p and q are integers and q ≠ 0.
We can get the decimal representation of the rational number p/q by long division division.
When we divide p by q using long division method either the remainder becomes zero or the remainder never becomes zero and we get a repeating string of remainders.
Case 1 (Remainder = 0) :
Let us express 7/16 in decimal form. Then 7/16 = 0.4375.
In this example, we observe that the remainder becomes zero after a few steps.
Also the decimal expansion of 7/16 terminates.
Similarly, using long division method we can express the following rational numbers in decimal form as
1/2 = 0.5
7/5 = 1.5
-8/25 = -0.32
In the above examples, the decimal expansion terminates or ends after a finite number of steps.
Case 2 ( Remainder ≠ 0) :
Does every rational number has a terminating decimal expansion?
Before answering the question, let us express 5/11 and 7/6 in decimal form.
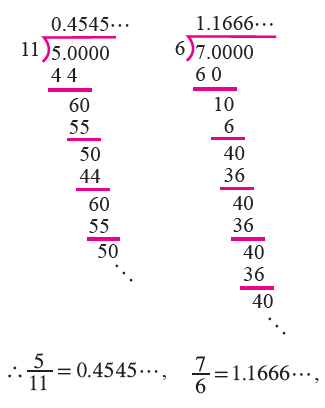
Thus, the decimal expansion of a rational number need not terminate.
In the above examples, we observe that the remainders never become zero. Also we note that the remainders repeat after some steps. So, we have a repeating (recurring) block of digits in the quotient.
To simplify the notation, we place a bar over the first block of the repeating (recurring) part and omit the remaining blocks.
So, we can write the expansion of 5/11 and 7/6 as follows..
The following table shows decimal representation of the reciprocals of the first ten natural numbers. We know that the reciprocal of a number n is 1/n. Obviously, the reciprocals of natural numbers are rational numbers.
Thus we see that,
A rational number can be expressed by either a terminating or a non-terminating and recurring (repeating) decimal expansion.
The converse of this statement is also true.
That is, if the decimal expansion of a number is terminating or non-terminating and recurring (repeating), then the number is a rational number.
Practice Questions
Express the following rational numbers as decimal numbers.
1) 3/4
2) 5/8
3) 9/16
4) 7/25
5) 47/99
6) 1/999
7) 26/45
8) 27/110
9) 2/3
10) 14/9
Answers
1) 3/4 = 0.75
2) 5/8 = 0.625
3) 9/16 = 0.5625
4) 7/25 = 0.0.28
5) 47/99 = 0.474747.........
6) 1/999 = 0.001001001........
7) 26/45 = 0.577777........
8) 27/110 = 0.2454545.........
9) 2/3 = 0.6666........
10) 14/9 = 1.5555..........
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
If you have any feedback about our math content, please mail us :
v4formath@gmail.com
We always appreciate your feedback.
You can also visit the following web pages on different stuff in math.
WORD PROBLEMS
Word problems on simple equations
Word problems on linear equations
Word problems on quadratic equations
Area and perimeter word problems
Word problems on direct variation and inverse variation
Word problems on comparing rates
Converting customary units word problems
Converting metric units word problems
Word problems on simple interest
Word problems on compound interest
Word problems on types of angles
Complementary and supplementary angles word problems
Trigonometry word problems
Markup and markdown word problems
Word problems on mixed fractrions
One step equation word problems
Linear inequalities word problems
Ratio and proportion word problems
Word problems on sets and venn diagrams
Pythagorean theorem word problems
Percent of a number word problems
Word problems on constant speed
Word problems on average speed
Word problems on sum of the angles of a triangle is 180 degree
OTHER TOPICS
Time, speed and distance shortcuts
Ratio and proportion shortcuts
Domain and range of rational functions
Domain and range of rational functions with holes
Graphing rational functions with holes
Converting repeating decimals in to fractions
Decimal representation of rational numbers
Finding square root using long division
L.C.M method to solve time and work problems
Translating the word problems in to algebraic expressions
Remainder when 2 power 256 is divided by 17
Remainder when 17 power 23 is divided by 16
Sum of all three digit numbers divisible by 6
Sum of all three digit numbers divisible by 7
Sum of all three digit numbers divisible by 8
Sum of all three digit numbers formed using 1, 3, 4
Sum of all three four digit numbers formed with non zero digits
Recent Articles
-
Practice Problems on Rationalizing Denominator
Sep 24, 20 07:37 PM
Practice Problems on Rationalizing Denominator
-
Worksheet on Operations with Surds
Sep 24, 20 07:32 PM
Worksheet on Operations with Surds
-
Exponents and Radicals Worksheet with Answers
Sep 24, 20 07:30 PM
Exponents and Radicals Worksheet with Answers
