DOMAIN AND RANGE OF TRIGONOMETRIC FUNCTIONS

To make the students to understand domain and range of a trigonometric function, we have given a table which clearly says the domain and range of trigonometric functions.

Domain of sin x and cos x

In any right angle triangle, we can define the following six trigonometric ratios.

sin x, cos x, csc x, sec x, tan x, cot x

In the above six trigonometric ratios, the first two trigonometric ratios sin x and cos x are defined for all real values of x. 

The two trigonometric ratios sin x and cos x are defined for all real values of x.

So, the domain for sin x and cos x is all real numbers.

Range of sin x and cos x

The diagrams given below clearly explains the range of sin x and cos x.

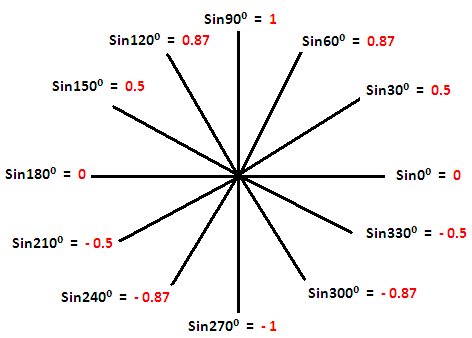
Range of sin x

Range of cos x

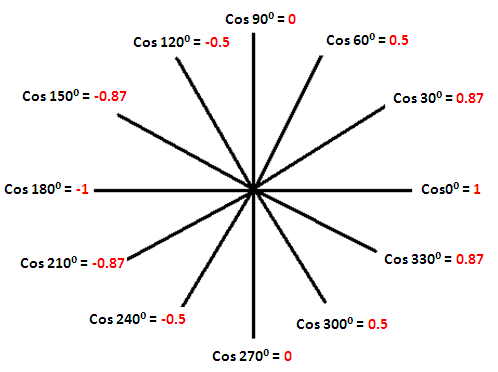
From the pictures above, it is very clear that the range of y = sin x and  y = cos x is

{y | -1 ≤ y ≤ 1}

Domain of csc x and sec x

We know that sin (kπ) = 0, cos [(2k+1)π] /2 = 0, here "k" is an integer. 

Then,

k  = ...........-2, -1, 0, 1, 2, ..........

For k  =  -2, 

sin (-2π)  =  0  and  cos (-3π/2)  =  0

For k  =  -1

sin (-π)  =  0  and  cos (-π/2)  =  0

For k  =  0,

sin (0)  =  0  and  cos (π/2)  =  0

For k  =  1,

sin (π)  =  0  and  cos (3π/2)  =  0

For k  =  2, 

sin (2π)  =  0  and  cos (5π/2)  =  0

Stuff 1 :

We know that csc x and sec x are the reciprocals of sin x and cos x respectively.

Let us see the values of csc x for

x  =  .......-2π, -π, 0, π, 2π, .........

csc(-2π)  =  1/sin(-2π)  =  1/0  = Undefined

csc(-π)  =  1/sin(-π)  =  1/0  = Undefined

csc(0)  =  1/sin(0)  =  1/0  = Undefined

csc(π)  =  1/sin(π)  =  1/0  = Undefined

csc(2π)  =  1/sin(2π)  =  1/0  = Undefined

From the above examples, it is very clear, that csc x is defined for all real values of x except

x  =  .......-2π, -π, 0, π, 2π, .........

So the domain of csc x is 

{x | x ≠ ...-2π, -π, 0, π, 2π, ..}

In the same way, domain of sec x is 

{x | x≠ ...-3π/2, -π/2, π/2, 3π/2, 5π/2 ...}

Range of csc x and sec x

Let y  =  csc x.

In the trigonometric function y  =  csc x, when plug values for x such that

x ∈ R - {.......-2π, -π, 0, π, 2π,.......},

we will get values for "y" which are out of the interval

(-1, 1) 

So the range of csc x is 

{y | y ≤ -1 or y ≥ 1}

In the same way, for the function y  =  sec x, when plug values for x such that        

x ∈ R - {.......-3π/2, -π/2, π/2, 3π/2, 5π/2.......},

we will get values for y which are out of the interval

(-1, 1) 

So the range of sec(x) is 

{ y | y ≤ -1 or y ≥ 1}

Domain of tan x and cot x

The trigonometric function tan x will become undefined for

x  =  [(2k + 1)π] / 2

here k is an integer.

Substituting k  =  ...........-2, -1, 0, 1, 2, .......... we get 

x  = ..........-3π/2, -π/2, π/2, 3π/2, 5π/2........

For the above values of x, tan x becomes undefined and tan x is defined for all other real values.

Therefore, domain of tan x is 

{x | x ≠......-3π/2, -π/2, π/2, 3π/2, 5π/2.....}

The trigonometric function cot x will become undefined for

x  =  kπ

here k" is an integer.

Substituting k  =  ...........-2, -1, 0, 1, 2, .......... we get 

x  = ..........-2π, -π, 0, π, 2π.......

For the above values of x, cot x becomes undefined and cot(x) is defined for all other real values.

So, the domain of cot x is

{x | x ≠......-2π, -π, 0, π, 2π.......}

Range of tan x and cot x

In the trigonometric function y  =  tan x, if we substitute  values for x such that

x ∈ R - {.......-3π/2, -π/2, π/2, 3π/2, 5π/2.....},

we will get all real values for "y" . 

So the range of tan x is 

All Real Values

In the same way, for cot x, if we substitute values for x such that        

x ∈ R - {.......-2π, -π, 0, π, 2π......},

we will get all values for y. 

So the range of cot x is

All Real Values

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.