FIND THE MODULUS AND ARGUMENT OF A COMPLEX NUMBER

Find the modulus and argument of a complex number :

Let (r, θ) be the polar co-ordinates of the point.

P = P(x, y) in the complex plane corresponding to the complex number

z = x + iy

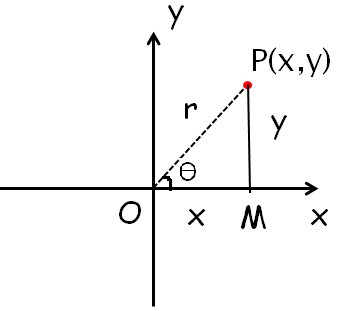
cos θ = Adjacent side/hypotenuse side ==> OM/MP ==> x/r

sin θ = Opposite side/hypotenuse side ==> PM/OP ==> y/r

x = r cos θ and y = r sin θ

Where r = √(x²+ y² )

|x + iy | is called the modulus or the absolute value of

z = x + iy denoted by mod z or | z | (i.e., the distance from the origin to the point z)

tan θ =y/x

θ = tan−1 y/x 

is called the amplitude or argument of z = x + iy

denoted by amp z or arg z and is measured as the angle which the line OP makes with the positive x-axis (in the anti clockwise sense).

How to find argument of complex number

Usually we have two methods to find the argument of a complex number

(i) Using the formula θ = tan−1 y/x  

here x and y are real and imaginary part of the complex number respectively.

This formula is applicable only if x and y are positive.

But the following method is used to find the argument of any complex number.  

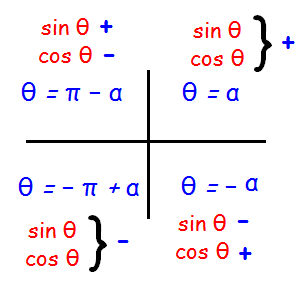
To find the modulus and argument for any complex number we have to equate them to the polar form

r (cos θ + i sin θ)

Here r stands for modulus and θ stands for argument

Let us see some example problems to understand how to find the modulus and argument of a complex number.

Find the modulus and argument of a complex number - Examples

Example 1 :

Find the modulus and argument of the complex number

- √2+i√2

Solution :

-√2 + i√2  =  r (cos θ  + i sin θ) ----(1)

Finding modulus :

r  =  √ [(-√2)² + √2²]

r  =  √(2 + 2)

r  =  √4

r  =  2

Finding Argument :

Apply the value of r in the first equation

- √2 + i√2  =  2(cos θ + i sin θ)

- √2+i√2  =  2 cos θ + i 2 sin θ

Equating the real and imaginary parts separately

Since sin θ is positive and cos θ is negative the required and θ lies in the second quadrant.

θ = Π - α

Here α is nothing but the angles of sin and cos for which we get the value 1/√2

θ = Π - (Π/4)

θ = (4Π-Π)/4 ==> 3Π/4

Modulus = 2 and argument = 3Π/4

Hence - √2 + i √2 = 2 (cos 3Π/4  + i sin 3Π/4)

Example 2 :

Find the modulus and argument of a complex number

1 + i √3

Solution :

1 + i √3 = r (cos θ  + i sin θ) ----(1)

Finding modulus :

r = √ [(1)² + √3²] = √(1 + 3) = √4 = 2

r = 2

Finding Argument :

Apply the value of r in the first equation

1 + i√3 =  2 (cos θ  + i sin θ)

1 + i√3 = 2 cos θ  + i 2 sin θ

Equating the real and imaginary parts separately

Since sin θ and cos θ are positive, the required and θ lies in the first quadrant.

θ = α

Here α is nothing but the angles of sin and cos for which we get the values 1/2 and √3/2 respectively.

θ = Π/3

Modulus = 2 and argument = Π/3

Hence - √2 + i √2 = 2 (cos Π/3  + i sin Π/3)

Example 3 :

Find the modulus and argument of the complex number

-1 - i√3

Solution :

-1 - i √3 = r (cos θ  + i sin θ) ----(1)

Finding modulus :

r  =  √ [(-1)² + (-√3)²] 

r  =  √(1 + 3) 

r  =  √4 

r  =  2

r  =  2

Finding Argument :

Apply the value of r in the first equation

-1 - i √3 =  2 (cos θ  + i sin θ)

-1 - i √3 = 2 cos θ  + i 2 sin θ

Equating the real and imaginary parts separately

Since sin θ and cos θ are negative the required and θ lies in the third quadrant.

θ = -Π + α

Here α is nothing but the angles of sin and cos for which we get the values √3/2 and 1/2 respectively.

θ = - Π + α

     = -Π + Π/3 ==> (-3Π+Π)/3 ==>-2Π/3

Modulus = 2 and argument  =  -2Π/3

Hence - 1 - i √3 = 2 (cos (-2Π/3)  + i sin (-2Π/3))

Example 4 :

Find the modulus and argument of the complex number

(√3+i)/(√3-i)

Solution :

Finding modulus :

|(√3+i)/(√3-i)|  =  [√(√3)²+1²]/[√(√3)²+(-1)²]

=  √4/√4

=  1

Finding Argument :

arg((√3+i)/(√3-i))  =  arg(√3+i) - arg(√3-i)

=  tan^-1(1/√3) - tan^-1(-1/√3)

=  Π/6 - (-Π/6)

=  Π/3

So, modulus is 1 and argument is Π/3.

Example 5 :

Find the modulus and argument of the complex number

-2/(1+i√3)

Solution :

Finding modulus :

|-2/(1+i√3)|  =  |-2|/[√1²+(√3)²]

=  2/√4

=  1/2

arg(-2/(1+i√3))  =  arg(-2) - arg(1+i√3)

Finding Argument :

We can consider -2 as -2+i0

=  tan^-1(0/2) - tan^-1(√3/1)

=  0 - Π/6

=  -Π/6

So, modulus is 1/2 and argument is -Π/6.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.