Finding Square Root of a Polynomial

FINDING SQUARE ROOT OF A POLYNOMIAL

Finding Square Root of a Polynomial :

In this section, you will learn how to find square root of a polynomial using long division.

Before look at the stuff finding square root of a polynomial, you are advised to look at the stuff finding square root of a number using long division step by step.

To have the stuff on finding square root of a number using long division,

Please click here

Note :

Before proceeding to find the square root of a polynomial, one has to ensure that the degrees of the variables are in descending or ascending order.

Finding Square Root of a Polynomial - Examples

Example 1 :

Find the square root of the following polynomial :

x⁴ - 4x³ + 10x² - 12x + 9

Solution :

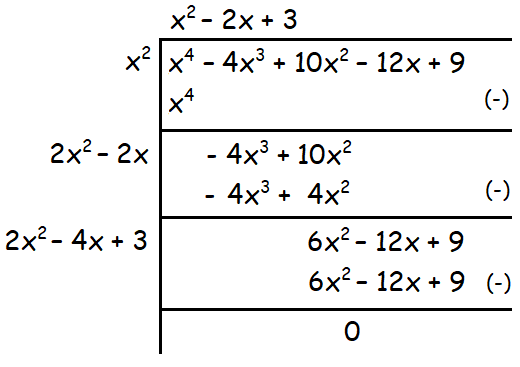
Therefore the square root of the given polynomial is

|x² - 2x + 3|

Example 2 :

Find the square root of the following polynomial :

4x⁴ + 8x³ + 8x² + 4x + 1

Solution :

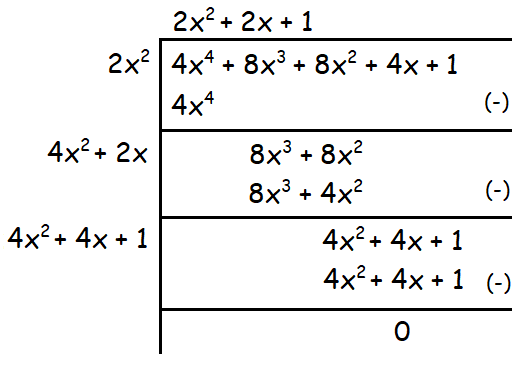
Therefore the square root of the given polynomial is

|2x² + 2x + 1|

Example 3 :

Find the square root of the following polynomial :

9x⁴ - 6x³ + 7x² - 2x + 1

Solution :

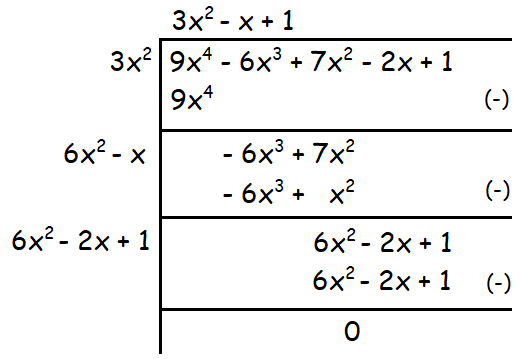
Therefore the square root of the given polynomial is

|3x² - x + 1|

Example 4 :

Find the square root of the following polynomial :

4 + 25x² - 12x - 24x³ + 16x⁴

Solution :

First arrange the term of the polynomial from highest exponent to lowest exponent and find the square root.

Then,

16x⁴ - 24x³ + 25x² - 12x + 4

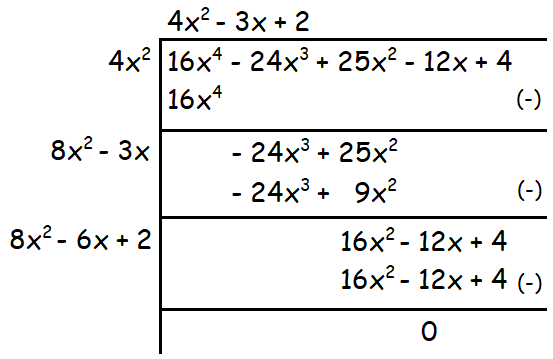
Therefore the square root of the given polynomial is

|4x² - 3x + 2|

Example 5 :

Find the values of a and b if the following polynomial is a perfect square

4x⁴ - 12x³ + 37x² + ax + b

Solution :

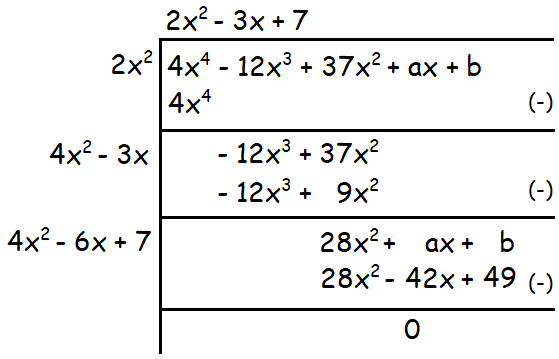
Because the given polynomial is a perfect square,

a + 42 = 0 and b - 49 = 0

Solving the above equations for a and b, we get

a = -42

b = 49

Example 6 :

Find the values of a and b if the following polynomial is a perfect square

x⁴ - 4x³ + 10x² - ax + b

Solution :

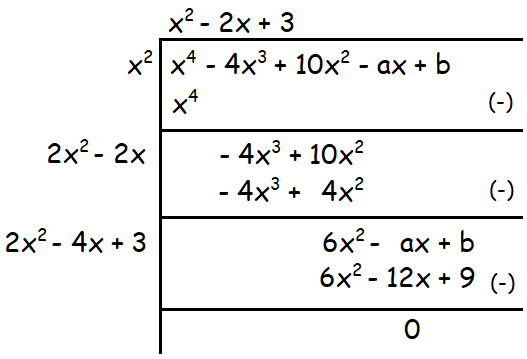
Because the given polynomial is a perfect square,

-a + 12 = 0 and b - 9 = 0

Solving the above equations for a and b, we get

a = 12

b = 9

Example 7 :

Find the values of a and b if the following polynomial is a perfect square

ax⁴ + bx³ + 109x² - 60x + 36

Solution :

Here a and b are being the coefficients of x⁴ and x³ respectively.

To solve for a and b, always they have to come at last.

So, write the given polynomial from lowest exponent to highest exponent.

36 - 60x + 109x² + bx³ + ax⁴

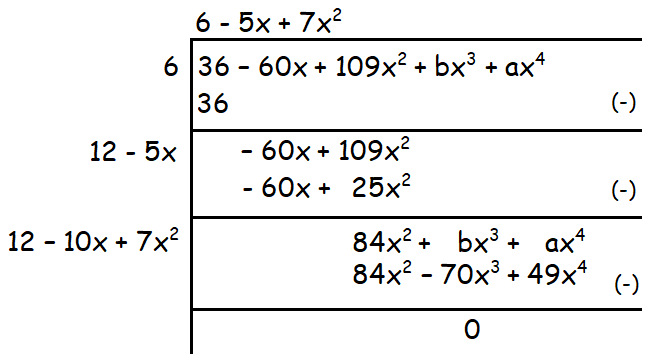
Because the given polynomial is a perfect square,

bx³ + 70x³ = 0 and ax⁴ - 49x⁴ = 0

Solve the above equations for a and b.

bx³ + 70x³ = 0

(b + 70)x³ = 0

Divide each side by x³.

b + 70 = 0

b = -70

ax⁴ - 49x⁴ = 0

(a - 49)x⁴ = 0

Divide each side by x⁴.

a - 49 = 0

a = 49

Therefore,

a = 49

b = -70

Example 8 :

Find the values of a and b if the following polynomial is a perfect square

ax⁴ - bx³ + 40x² + 24x + 36

Solution :

Here a and b are being the coefficients of x⁴ and x³ respectively.

To solve for a and b, always they have to come at last.

So, write the given polynomial from lowest exponent to highest exponent.

36 + 24x + 40x² - bx³ + ax⁴

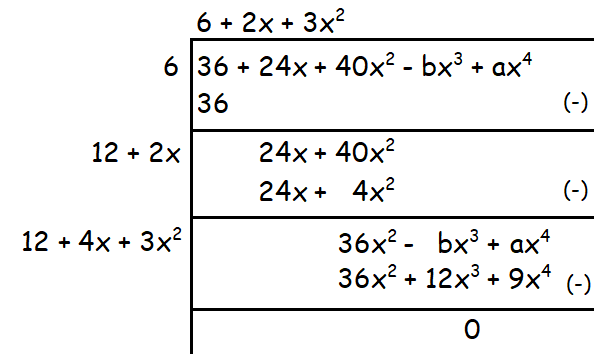
Because the given polynomial is a perfect square,

-bx³ - 12x³ = 0 and ax⁴ - 9x⁴ = 0

Solve the above equations for a and b.

-bx³ - 12x³ = 0

(b + 12)(-x³) = 0

Divide each side by (-x³).

b + 12 = 0

b = -12

ax⁴ - 9x⁴ = 0

(a - 9)x⁴ = 0

Divide each side by x⁴.

a - 9 = 0

a = 9

Therefore,

a = 9

b = -12

After having gone through the stuff given above, we hope that the students would have understood, how to find square root of a polynomial using long division.

Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search here.

HTML Comment Box is loading comments...

You can also visit our following web pages on different stuff in math.

ALGEBRA

Variables and constants

Writing and evaluating expressions

Solving linear equations using elimination method

Solving linear equations using substitution method

Solving linear equations using cross multiplication method

Solving one step equations

Solving quadratic equations by factoring

Solving quadratic equations by quadratic formula