FINDING UNKNOWN ANGLE MEASURES WORKSHEET

Problem 1 :

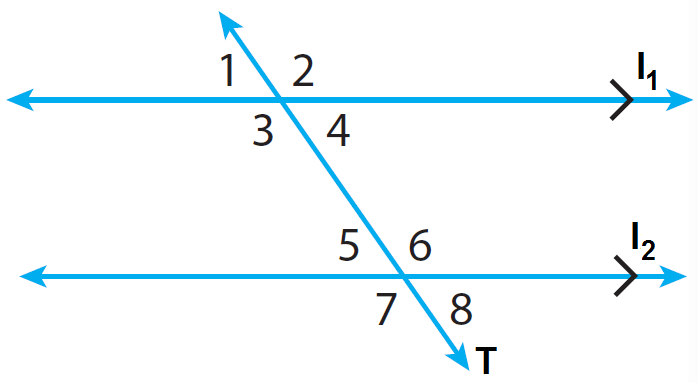
In the diagram given below, the lines l₁ and l₂ are parallel and the line T is transversal. Find m∠2 when m∠7 = 120°.

Problem 2 :

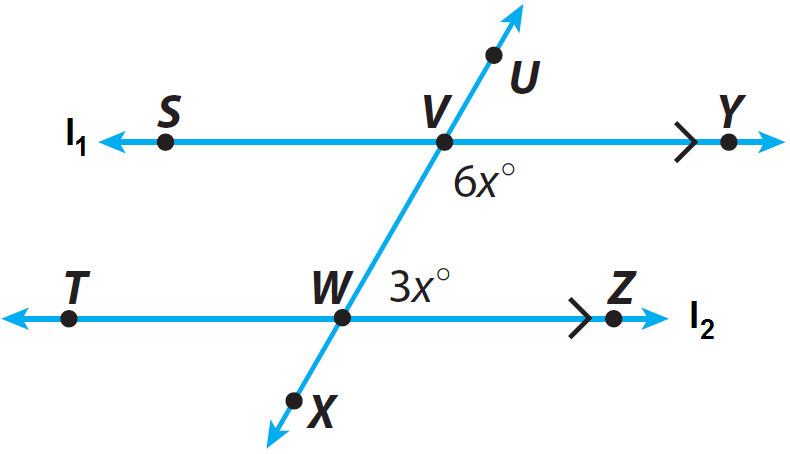
In the diagram given below, the lines l₁ and l₂ are parallel and the line T is transversal. Find m∠VWZ.

Problem 3 :

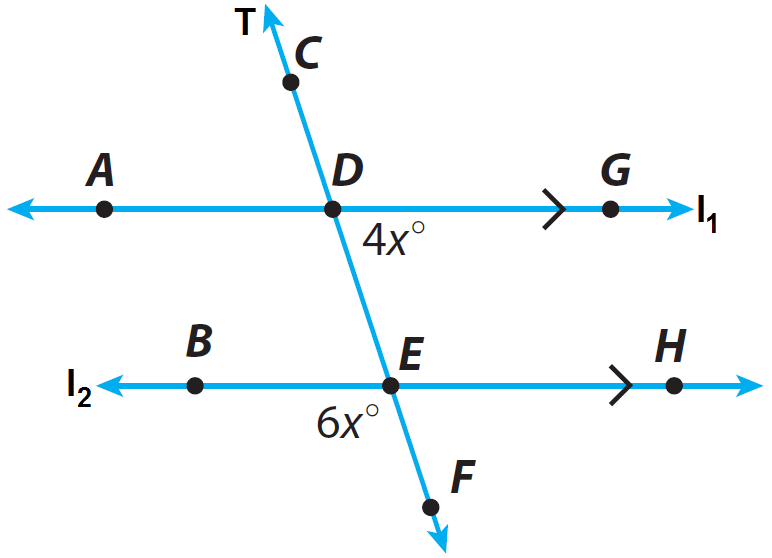
In the diagram given below, the lines l₁ and l₂ are parallel and the line T is transversal. Find m∠GDE.

Problem 4 :

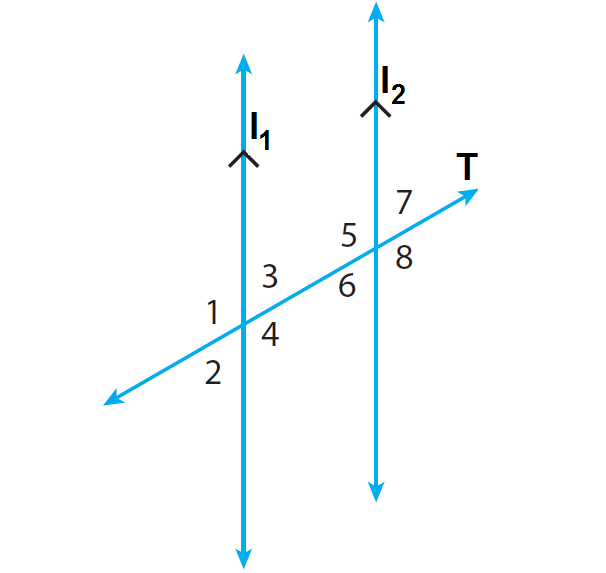
In the diagram given below, the lines l₁ and l₂ are parallel and the line T is transversal. Find m∠3 when m∠7 = 65°.

Answers

1. Answer :

Step 1 :

In the above diagram, m∠2 and m∠7 are alternate interior angles. 

Step 2 :

When two parallel lines are cut by a transversal, alternate interior angles are congruent.

So, we have 

m∠2 = m∠7

m∠2 = 120°

2. Answer :

Step 1 :

In the above diagram, m∠VWZ and m∠YVW are same-side interior angles. 

Step 2 :

When two parallel lines are cut by a transversal, same-side interior angles are supplementary.

So, we have 

m∠VWZ + m∠YVW = 180°

Step 3 :

From the diagram given above, we have m∠VWZ = 3x and m∠YVW = 6x. So, replace m∠VWZ by 3x and m∠YVW by 6x.

3x° + 6x° = 180°

Combine like terms.

9x° = 180°

Divide both sides by 9.

x° = 20°

Step 4 :

Substitute x = 20° into m∠VWZ = 3x°. 

m∠VWZ = 3 · 20°

m∠VWZ = 60°

3. Answer :

Step 1 :

In the above diagram, m∠GDE and m∠ADE are angles on the straight line l₁. 

So, we have

m∠GDE + m∠ADE = 180° -----(1)

Step 2 :

In the above diagram, m∠ADE and m∠BEF are corresponding angles and corresponding angles are always congruent. 

So, we have 

m∠ADE = m∠BEF

Step 3 :

In (1) replace m∠ADE by m∠BEF

(1) -----> m∠GDE + m∠BEF  =  180° 

Step 4 :

From the diagram given above, we have m∠GDE = 4x and m∠BEF = 6x. So, replace m∠GDE by 4x and m∠BEF by 6x.

4x° + 6x°  =  180°

Combine like terms.

10x°  =  180°

x°  =  18°

Step 5 :

Substitute x° = 18° into m∠GDE = 4x°. 

m∠GDE = 4 · 18°

m∠GDE = 72°

4. Answer :

Step 1 :

In the above diagram, m∠6 and m∠7 are vertially opposite angles and they are congruent.

m∠6 = m∠7

m∠6 = 65°

Step 2 :

In the above diagram, m∠3 and m∠6 are alternate interior angles and they are congruent.

m∠3 = m∠6

m∠3 = 65°

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.