LIKE TERMS AND UNLIKE TERMS

Like Terms or Similar Terms: 

Like terms are the terms which have the same variables with same exponent for each variable.

Example :

7x, 3x, - 4x

Unlike Terms or Dissimilar Terms: 

Unlike terms are the terms which have same variables or different variables. 

If they have same variables, the exponents will not be same. 

Example :

9x², 5xy, - 4xy², y, 6

More clearly, 

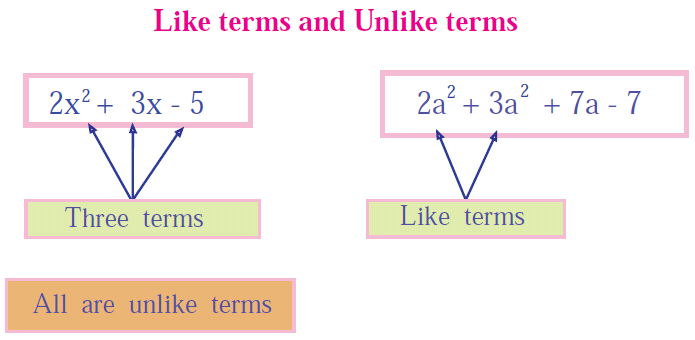
Why should we know the difference between like terms and unlike terms ?

To do addition and subtraction of algebraic expression, we have to know the difference between like and unlike terms.

Because, in algebraic expression, we can do addition and subtraction only on like terms not on unlike terms.

Some More Stuff on Like Terms and Unlike Terms

Adding or subtracting polynomials is nothing but combining the like terms. Here we give step by step explanation for adding and subtracting polynomials.

Let us look at some examples to have better understanding on addition and subtraction of algebraic expression with like terms. 

Example 1 :

Add :  

3x³  +  x² -  2   and  2x²  + 5x + 5

Solution : 

First we have to arrange the like terms column wise and add them.  

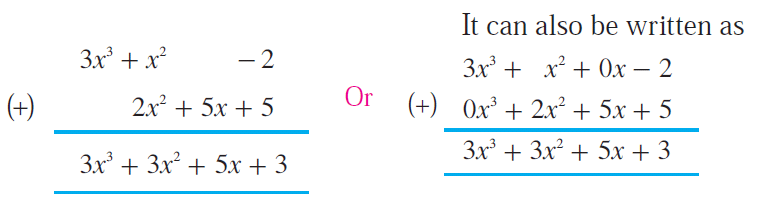
Observe the important points related to the above work. 

1. We have written the term 2x² of the second polynomial below the corresponding term x² of the first polynomial.

(Because x² and 2x² are like terms and they can be combined)

2. Similarly, the constant term +5 is placed below the constant term – 2.

3. Since the term x in the first polynomial and the term x³ in the second polynomial do not exist, their respective places have been left blank to  facilitate the process of addition. Or, for the non existing terms, we annex the terms with zero coefficients.

Example 2 :

Find out the sum of the polynomials : 

3x - y, 2y - 2x, and x + y. 

Solution : 

We can find out the sum of the given polynomials using either column method of addition or row method of addition as explained below. 

Once they are written in the above methods, we have to combine the like terms.

Example 3 :

Subtract 5xy from 8xy. 

Solution : 

Example 4 :

Subtract (3c + 7d²)  from  (5c - d²).

Solution : 

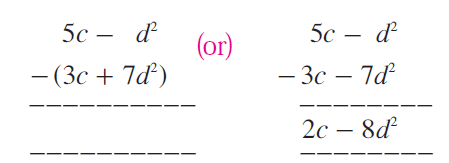
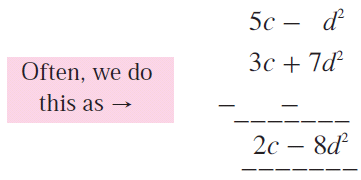
Alternatively, this can also be done as :

(5c - d²) - (3c + 7d²)  =  5c - d²  -  3c - 7d² 

=  (5c - 3c) + (-d² - 7d²)

=  2c  + (-8d²)

=  2c   - 8d²

Example 5 :

Subtract (2x² + 2y² - 6)  from  (3x² - 7y² + 9)

Solution : 

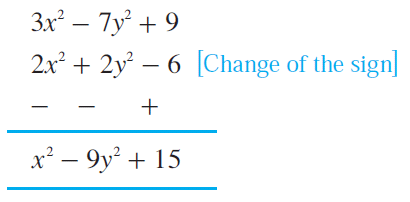
Example 6 :

Add :

(7p³ +  4p²- 8p + 1 ) and (3p³- 5p²- 10p + 5)

Solution : 

Step 1 :

The two given polynomials are already in the arranged form.So we can leave it as it is.

=  (7p³ +  4p²- 8p + 1 ) and (3p³- 5p²- 10p + 5)

Step 2 :

Now we have to write the like terms together starting from the highest power to lowest power.

=  7p³ + 3p³ + 4p²- 5p²- 8p - 10p + 1 + 5

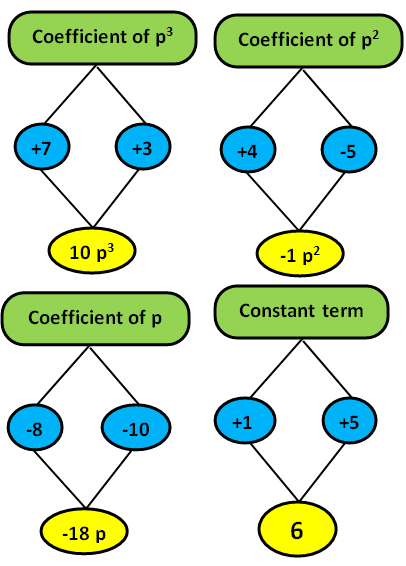
So, the final answer is

10p³- 1p²- 18p + 6.

Example 7 :

Add :

(2x³ + 5x² - 2x + 7) and (x³ + 4x² - x + 6)

Solution : 

=  (2x³ + 5x² - 2x + 7) + (x³ + 4x² - x + 6)

=  2x³ + 5x² - 2x + 7 + x³ + 4x² - x + 6

=  2x³ + x³ + 5x² + 4x² - 2x - x + 7 + 6

=  3x³ + 9x² - 3x + 13

Example 8 :

Add :

(3x³ - 2x² - x + 4) and (2x³ + 7x² - 3x - 3)

Solution : 

=  (3x³ - 2x² - x + 4) + (2x³ + 7x² - 3x - 3)

=  3x³ - 2x² - x + 4 + 2x³ + 7x² - 3 x - 3

=  3x³ + 2x³ - 2x² + 7x² - x - 3x + 4 - 3

=  5x³ + 5x² - 4x + 1 

Example 9 :

Add :

2(x³ - x² + 6x - 2) and (5x⁶ + 7x⁵ - 3x - 3)

Solution : 

=  2(x³ - x² + 6x - 2) + (5x⁶ + 7x⁵ - 3x - 3)

=  2x³ - 2x² + 12x - 4 + 5x⁶ + 7x⁵ - 3x - 3

=  5x⁶ + 7x⁵ + 2x³ - 2x² + 12x - 3x - 4 - 3

=  5x⁶ + 7x⁶ + 2x³ - 2x² + 9x - 7

Example 10 :

Add :

-1(x⁶ + x³ + 6x² - 2) and 2(5x⁶ + 7x⁵ - 3x - 3)

Solution : 

=  -1(x⁶ + x³ + 6x² - 2) + 2(5x⁶ + 7x⁵ - 3x - 3)

=  -x⁶ - x³ - 6x² + 2 + 10x⁶ + 14x⁵ - 6x - 6

=  -x⁶ + 10x⁶ + 14x⁵ - x³ - 6x² - 6x + 2 - 6

=  9x⁶ + 14x⁵ - x³ - 6x² - 6x - 4

Example 11 :

Add :

5(5x⁶ + 2x³ - 6x² - 2) + 6(-3x⁶ + 2x⁵ + 2x + 1)

Solution : 

=  5(5x⁶ + 2x³ - 6x² - 2) + 6(-3x⁶ + 2x⁵ + 2x + 1)

=  25x⁶ + 10x³ - 30x² - 10 -18x⁶ + 12x⁵ + 12x + 6

=  25x⁶ -18x⁶ + 12x⁵ + 10x³ - 30x² + 12x -10 + 6

=  7x⁶ + 12x⁵ + 10x³ - 30x² + 12x - 4

Example 12 :

Add :

-2(2x⁴ - 2x³ - x² + 5) and 3(2x⁴ - 2x² - 3)

Solution :

=  -2(2x⁴ - 2x³ - x² + 5) +  3(2x⁴ - 2x² - 3)

=  -4x⁴ + 4x³ + 2x² -10 +  6x⁴ - 6x² - 9

=  -4x⁴ + 6x⁴ + 4x³ + 2x² - 6x² -10 - 9

=  2x⁴ + 4x³ - 4x² - 19

Example 13 :

Add :

5(x⁴ - x³ + 5) and  2(x⁴ - 5x² - 7)

Solution :

=  5(x⁴ - x³ + 5) +  2(x⁴ - 5x² - 7)

=  5x⁴ - 5x³ + 25 + 2x⁴ - 10x² - 14

=  5x⁴ + 2x⁴ - 5x³ - 10x² + 25 - 14

=  7x⁴ - 5x³ - 10x² + 11

Example 14 : 

Add :

3(6x⁴ - 2x³ - 3) and 2(2x⁴ - x² - 8)

Solution : 

=  3(6x⁴ - 2x³ - 3) + 2(2x⁴ - x² - 8)

=  18x⁴ - 6x³ - 9 + 4x⁴ - 2x² - 16

=  18x⁴ + 4x⁴ - 6x³ - 2x² - 9 - 16

=  22x⁴ - 6x³ -2x² - 25

Example 15 :

Add :

(6x⁷ - 2x⁶ - 3x³ + 2x²) and 2(2x⁴ + 5x⁷ + 3x⁶ + x³ + x²)

Solution : 

=  (6x⁷ - 2x⁶ - 3x³ + 2x²) + 2(2x⁴ + 5x⁷ + 3x⁶ + x³ + x²)

=  6x⁷ - 2x⁶ - 3x³ + 2x² + 4x⁴ + 10x⁷ + 6x⁶ + 2x³ + 2x²

=  6x⁷ + 10x⁷- 2x⁶ + 6x⁶ + 4x⁴ - 3x³ + 2x³ + 2x² + 2x²

=  16x⁷ + 4x⁶ + 4x⁴ - x³ + 4x²

Example 16 :

Add :

(x⁷ - 3x⁶ - 2x³ + x²) and 5(3x⁴ + 15x⁷ + 4x⁶ + 2x³ + 6x²)

Solution : 

=  (x⁷ - 3x⁶ - 2x³ + x²) + 5(3x⁴ + 15x⁷ + 4x⁶ + 2x³ + 6x²)

=  x⁷ - 3x⁶ - 2x³ + x² + 15x⁴ + 75x⁷ + 20x⁶ + 10x³ + 30x²

=  x⁷ + 75x⁷- 3x⁶ + 20x⁶ - 2x³ + 10x³ + x² + 30x²

=  76x⁷ + 17x⁶ + 8x³ + 31x²

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.