LINEAR QUADRATIC SYSTEMS

A linear quadratic system is a system containing one linear equation and one quadratic equation which may be one straight line and one parabola, or one straight line and one circle.

Example 1 : 

Solve y = 2x² and y = - x + 6 graphically. 

Solution : 

First let us make a table of values to graph y = 2x²

We can get the following points from the table.

(–3, 18), (–2, 8),(–1,2), (0, 0), (1, 2), (2, 8), (3, 18) ----- (1)

Now,  let us make a table of values to graph y = -x + 6

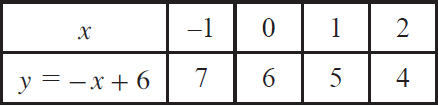
We can get the following points from the table.

(–1, 7), (0, 6), (1, 5), (1, 5), (2, 4) ----- (2)

Plotting the points which we have in (1) and (2), we get the graph of y = 2x² and y = -x + 6

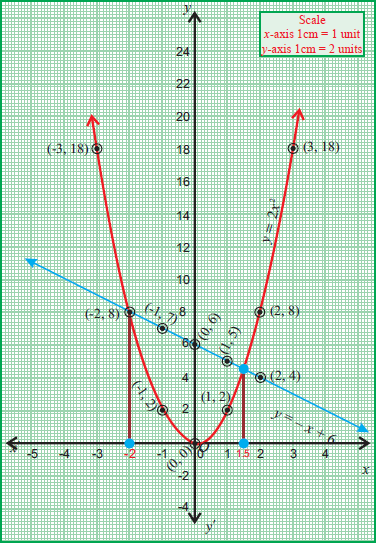
From the graph, the points of intersection or the two solutions for the given system are

(-2, 8) and (1.5, 4.5)

Example 2 :  

Solve y = x² + 3x +2 and y =  x - 2 graphically. 

Solution : 

First let us make a table of values to graph y = x² + 3x +2

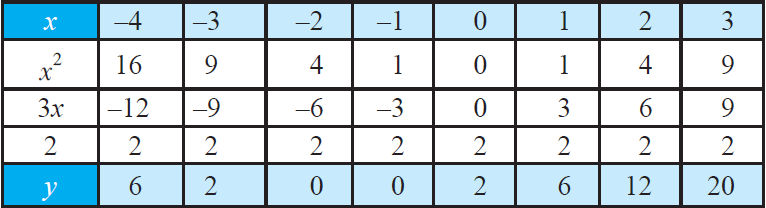
We can get the following points from the table.

(–4, 6), (–3, 2), (–2, 0), (–1, 0), (0, 2), (1, 6), (2, 12) and            (3, 20) ----- (1)

Now,  let us make a table of values to graph y = x - 2

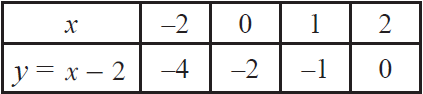
We can get the following points from the table.

(-2, -4), (0, -2), (1, -1), (2, 0) ----- (2)

Plotting the points which we have in (1) and (2), we get the graph of y = x² + 3x +2 and y = x - 2

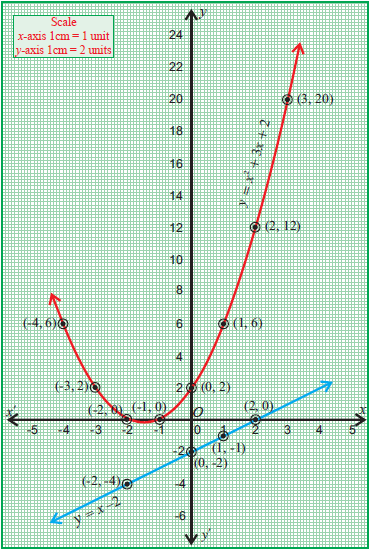
In the above graph, the straight line y = x - 2 does not intersect y = x² + 3x +2. 

Hence, there is no solution for the given system.

Example 3 : 

Draw the graph of y = 2x² and hence solve 2x²+x-6 = 0.

Solution : 

First let us make a table of values to graph y = 2x²

We can get the following points from the table.

(–3, 18), (–2, 8),(–1,2), (0, 0), (1, 2), (2, 8), (3, 18) ----- (1)

Now, let us take the quadratic equation 2x²+x-6 = 0.

Form the first equation, we know y = 2x². 

So, plugging 2x² = y in (2x²+x-6 = 0), we get 

y + x - 6 = 0

y  =  -x + 6

Now,  let us make a table of values to graph y = -x + 6

We can get the following points from the table.

(–1, 7), (0, 6), (1, 5), (1, 5), (2, 4) ----- (2)

Thus, the roots of 2x² + x - 6 = 0 are nothing but the x - coordinates of point of intersection of y = 2x² and y  = -x  + 6.

Plotting the points which we have in (1) and (2), we get the graph of y = 2x² and y = -x + 6

In the graph above, the points of intersection of the line and the parabola are

(-2, 8) and (1.5, 4.5)

The x-coordinates in the points of intersection are -2 and 1.5. 

Hence, the two solutions of the equation 2x²+x-6 = 0 are 

-2 and 1.5 

Example 4 : 

Draw the graph of y = x² + 3x + 2 and use it to solve the equation x² + 2x + 4 = 0.

Solution : 

First let us make a table of values to graph y = x² + 3x + 2

We can get the following points from the table.

(–4, 6), (–3, 2), (–2, 0), (–1, 0), (0, 2), (1, 6), (2, 12) and            (3, 20) ----- (1)

Now, let us take the quadratic equation x²+ 2x + 4 = 0

x²+ 2x + 4 = 0

x²+ (3x-x) + (2+2) = 0

x²+ 3x + 2 - x + 2 = 0

Form the first equation, we know y = x² + 3x + 2. 

So, plugging x² + 3x + 2 = y in (x²+ 3x + 2 - x + 2 = 0), we get 

y - x + 2 = 0

y  =  x - 2

Now,  let us make a table of values to graph y = x - 2

We can get the following points from the table.

(-2, -4), (0, -2), (1, -1), (2, 0) ----- (2)

Thus, the roots of x² + 2x + 4 = 0 are obtained from the points of intersection of y = x - 2 and y  = x² + 3x + 2

Plotting the points which we have in (1) and (2), we get the graph of y = x² + 3x +2 and y = x - 2

In the above graph, the straight line y = x - 2 does not intersect y = x² + 3x +2. 

Hence, the quadratic equation x² + x + 4 = 0 has no real roots. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.