PARALLELOGRAM WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Find the lengths of SR and SK in the parallelogram shown below. Explain your reasoning.
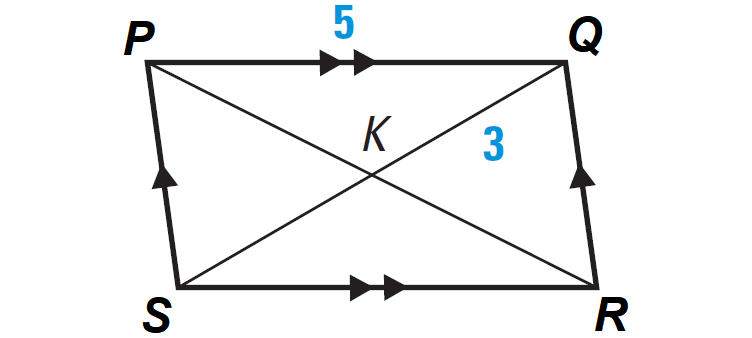
Problem 2 :
Find the measures of ∠C and ∠B in the parallelogram ABCD.
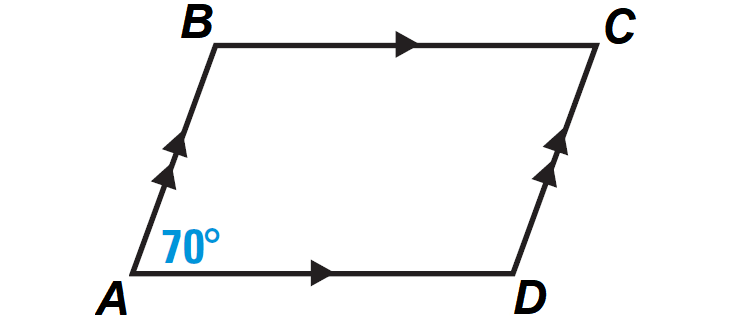
Problem 3 :
Find the value of x in the parallelogram ABCD shown below.
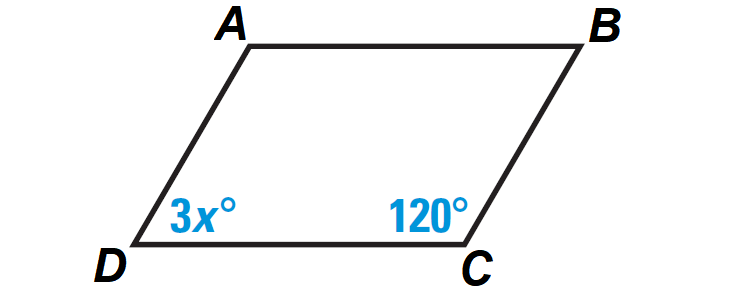
Problem 4 :
In the diagram shown below, ABCD and AEFG are parallelograms. Prove that m∠1 ≅ m∠3.
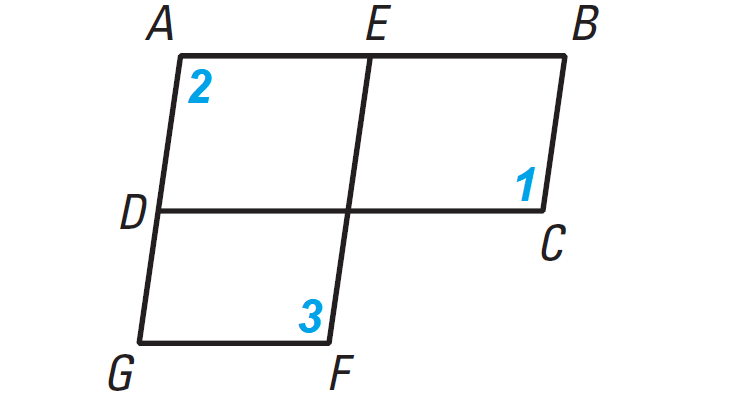
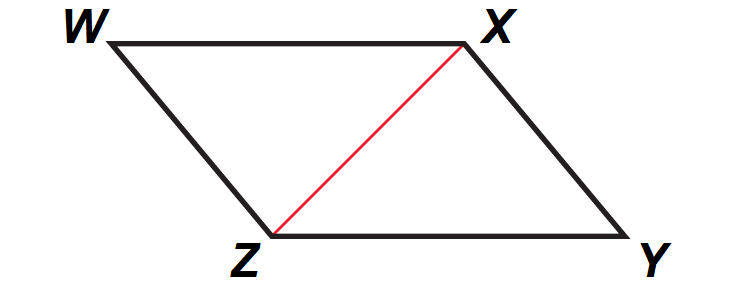
Problem 5 :
In the parallelogram ABCD shown below, prove that WX ≅ YZ and WZ ≅ XY.

Answers
1. Answer :

Finding the length of SR :
By Theorem, opposite sides of a parallelogram are congruent.
So, we have
SR = PQ
From the diagram, PQ = 5.
SR = 5
Finding the length of SK :
By Theorem, diagonals of a parallelogram bisect each other.
So, we have
SK = QK
From the diagram, QK = 3.
SK = 3
2. Answer :

Finding the measure of ∠C :
By Theorem, opposite angles of a parallelogram are congruent.
So, we have
m∠C = m∠A
From the diagram, m∠A = 70°.
m∠C = 70°
Finding the measure of ∠B :
By Theorem, consecutive angles of a parallelogram are supplementary.
So, we have
m∠A + m∠B = 180°
From the diagram, m∠A = 70°.
70° + m∠B = 180°
Subtract 70° from both sides.
m∠B = 110°
3. Answer :

By Theorem, consecutive angles of a parallelogram are supplementary.
So, we have
m∠D + m∠C = 180°
Substitute m∠D = 3x° and m∠C = 120°.
3x° + 120° = 180°
Subtract 120° from both sides.
3x° = 60°
3x = 60
Divide both sides by 3.
x = 20
4. Answer :

Plan : Show that both angles are congruent to m∠2. Then use the Transitive Property of Congruence.
|
Statements ABCD is a parallelogram AEFG is a parallelogram aaaaa m∠1 ≅ m∠2 aaa aaaaa m∠2 ≅ m∠3 aaa m∠1 ≅ m∠2 |
Reasons aaaaaaaaa Given aaaaaaa aaaaaaaaaaaaaaaaaaaaaaa Opposite angles of a parallelogram are congruent. Transitive property of congruence. |
5. Answer :

|
Statements aaaaaa WXYZ is a aaaaa aaaa parallelogram aaaa aaaaaa Draw XZ aaaaaa aaaaaaaaaaaaaaaaaaaaa aaaaaaaaaaaaaaaaaaaaa WX || YZ, WZ || XY aa m∠WXZ ≅ m∠YZX a aa m∠WZX ≅ m∠YXZ aaaaaa ZX ≅ ZX aaaaa aaaaaaaaaaaaaaaaaaaaa ΔWZX ≅ ΔYXZ WX ≅ YZ, WZ ≅ XY |
Reasons aaaaaaaaaa Given aaaaaaaaa aaaaaaaaaaaaaaaaaaaaaaaa aaThrough any two points there exists exactly one a aaaaaaaaa line. Definition of parallelogram Alternate Interior Angles Theorem Reflexive Property of Congruence ASA Congruence Postulate Corresponding parts of congruent triangles are congruent |
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 29, 25 04:21 AM
10 Hard SAT Math Questions (Part - 38) -
10 Hard SAT Math Questions (Part - 39)
Dec 28, 25 11:20 PM
10 Hard SAT Math Questions (Part - 39) -
10 Hard SAT Math Questions (Part - 41)
Dec 28, 25 06:05 PM
10 Hard SAT Math Questions (Part - 41)

