PROPERTIES OF QUADRATIC EQUATIONS

1. The zeros of a quadratic function f(x) = ax²+ bx + c are nothing but the two values of 'x' when

f(x) = 0  or  ax² + bx + c = 0

Here, ax² + bx + c  =  0 is called quadratic equation.

Finding the two zeros of a quadratic function or solving the quadratic equation are the same thing.  

2. The standard form of a quadratic equation is 

ax² + bx + c = 0

3. There are three methods to find the two zeros of a quadratic equations. 

They are, 

(i) Factoring

(ii) Quadratic formula

(iii) Completing square

4. If the two zeros of a quadratic equation are irrational, then the two zeros (roots) will occur in conjugate pairs. That is, if (m + √n) is a root, then (m - √n) is the other root of the same equation. 

5. The sum of the zeros of the quadratic equation in standard form ax²+ bx + c = 0 is -b/a. 

6. The product of the zeros of the quadratic equation in standard form ax²+ bx + c = 0 is c/a.

7. If two zeros of a quadratic equation ax²+ bx + c = 0 are reciprocal to each other, then their product is 1 or

c = a 

8. If two zeros of a quadratic equation ax²+ bx + c = 0 are equal in magnitude, but opposite in sign, then their sum is equal to zero or 

b = 0

9. If we know the two zeros  of a quadratic equation, the formula given below can be used to form the quadratic equation. 

x² - (Sum of the roots)x + product of the roots = 0

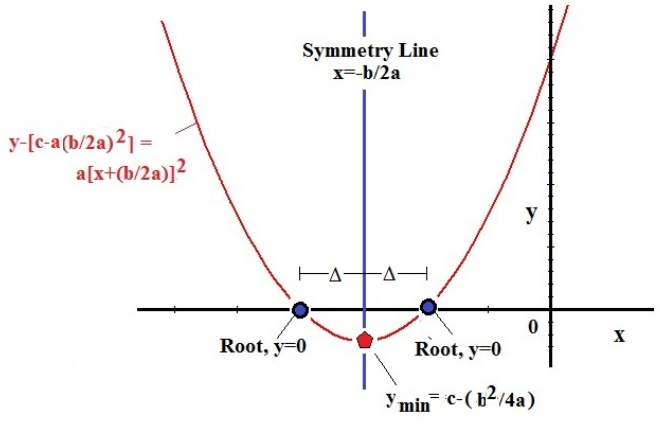
10. The graph of any quadratic equation will be a parabola. In f(x) = ax² + bx + c, if a > 0, the parabola opens up and if a < 0, the parabola opens down. 

11. The zeros of a quadratic equation are the x-coordinates of the points where the parabola (graph of quadratic a function) cuts x-axis.

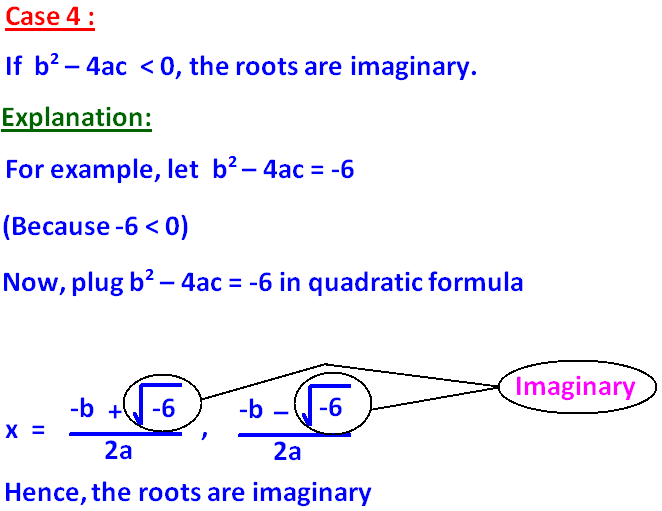
12. If the two zeros of a quadratic equation are imaginary, then the graph (parabola) will never intersect x - axis. 

13. The two x-intercepts of a parabola (graph of a quadratic function) are the zeros of the quadratic equation. 

14. x- coordinate of the vertex of the parabola is -b/2a and the vertex is (-b/2a, f(-b/2a)). 

15. To know at where the parabola cuts y-axis or y-intercept of the parabola, we have to plug x = 0 in the given quadratic function.

16. The discriminant b² - 4ac  discriminates the nature of the zeros of the quadratic equation ax² + bx + c = 0.

Let us see how this discriminant  'b² - 4ac' can be used to know the nature of the roots of a quadratic equation. 

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.