REFLECTIONS IN THE COORDINATE PLANE WORKSHEET

Problem 1 :

Graph (3, -2). Then fold your coordinate plane along the y-axis and find the reflection of (3, -2). Record the coordinates of the new point in the table.

Problem 2 :

Graph (3, -2). Then fold your coordinate plane along the x-axis and find the reflection of (3, -2). Record the coordinates of the new point in the table.

Problem 3 :

What is the relationship between the coordinates of a point and the coordinates of its reflection across each axis?

Problem 4 :

Let A(-2, 1), B(2, 4) and C(4, 2) be the three vertices of a triangle. If this triangle is reflected about x-axis, what will be the new vertices A', B' and C'?

Problem 5 :

Let A (2, 2), B (4, 4) and C(5, 1) be the three vertices of a triangle. If this triangle is reflected about y-axis, what will be the new vertices A', B' and C'?

Problem 6 :

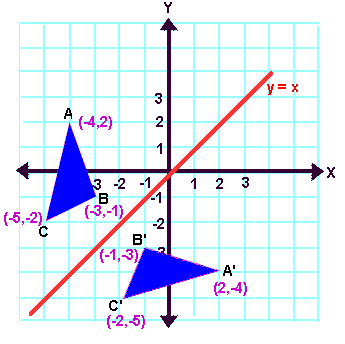
Let A (-4, 2), B (-3, -1) and C(-5, -2) be the three vertices of a triangle. If this triangle is reflected about the line y = x, what will be the new vertices A', B' and C'?

Problem 7 :

Let A (-5, 3), B (-3, 0) and C(-5, -2) be the three vertices of a triangle. If this triangle is reflected about the line x = -2, what will be the new vertices A', B' and C'?

1. Answer :

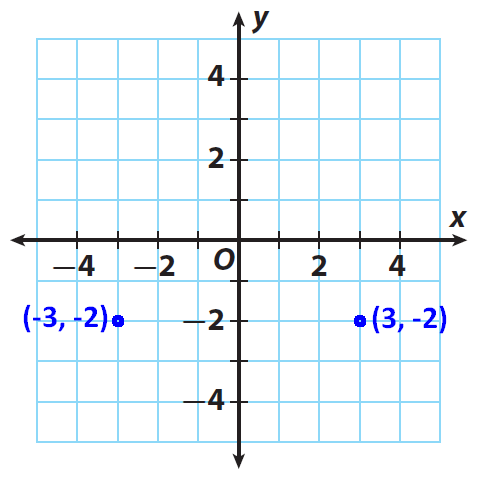
2. Answer :

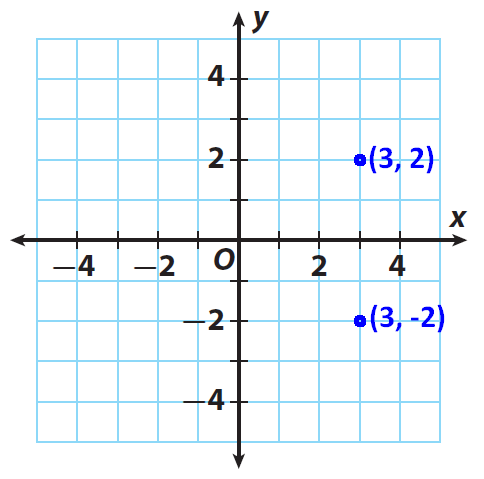
Based on the above answers, we can do the answer given below.

3. Answer :

Across y-axis :

Opposite x-coordinate and same y-coordinate as the original point.

Across x-axis :

Same x-coordinate and opposite y-coordinate as the original point.

4. Answer :

Step 1 :

First we have to know the correct rule that we have to apply in this problem.

Step 2 :

Here triangle is reflected about x - axis. So the rule that we have to apply here is (x , y) ----> (x , -y).

Step 3 :

Based on the rule given in step 1, we have to find the vertices of the reflected triangle A'B'C'

Step 4 :

(x, y) ----> (x, -y)

A(-2, 1) ----> A'(-2, -1)

B(2, 4) ----> B'(2, -4)

C(4, 2) ----> C'(4, -2)

Step 5 :

Vertices of the reflected triangle are

A'(-2, -1), B(2, -4) and C'(4, -2)

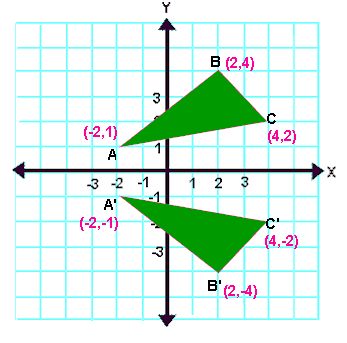
5. Answer :

Rule : (x, y) ----> (-x, y)

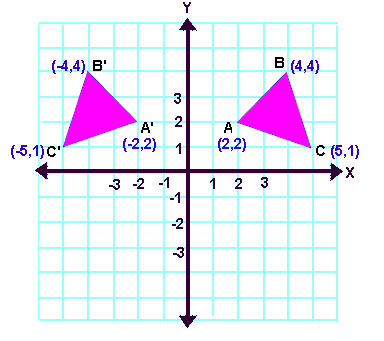
6. Answer :

Rule : (x, y) ----> (-y, -x)

7. Answer :

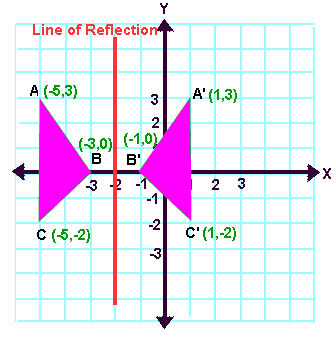
When we look at the above figure, it is very clear that each point of a reflected image A'B'C' is at the same distance from the line of reflection as the corresponding point of the original figure.

In other words, the line x = -2 (line of reflection) lies directly in the middle between the original figure and its image.

And also, the line x = -2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image.

Students can keep this idea in mind when they are working with lines of reflections which are neither the x-axis nor the y-axis.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.