REPRESENTATION OF RATIONAL NUMBERS ON NUMBER LINE

A number that is expressed in the form a/b is called as rational number.

Here both "a" and "b" are integers and also b ≠ 0.

We all know, how to represent integers on the number line.

In the picture given below, the two integers 3 and 4 are represented on a number line. 

In the picture given below, the integers -1, 0, 1, 2 and 3 are represented on a number line. 

On a number line, can you find any integer between 1 and 2 ?

No.

But, between any two integers, we can represent rational rational numbers.

For example, between 0 and 1, we can represent rational numbers 1/10, 2/10, 3/10, .....which can be written as 0.1, 0.2, 0.3,.....

Similarly, we know that the numbers 1/4, 1/2, 3/4 can be represented between 0 and 1. These are rational numbers which can be written as 0.25, 0.5, 0.75 respectively.

Now, consider 2/5 and 4/5.

Can you find any rational number between 2/5 and 4/5 ?

Yes. There is a rational number 3/5

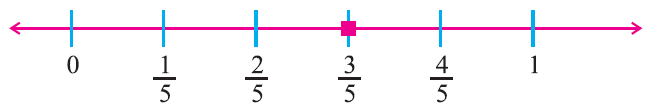
In the same manner, we know that the numbers 1/5, 2/5, 3/5 and 4/5 are lying between 0 and 1. 

Can you find more rational numbers between 2/5 and 3/5 ?

Yes. We write 2/5 as 20/50 and 3/5 as 30/50, then we can find many rational numbers between them.

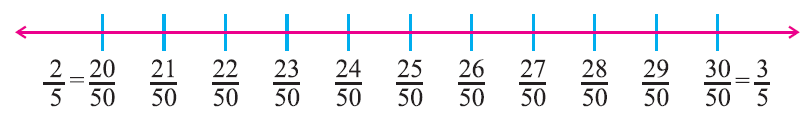
We can find nine rational numbers 21/50, 22/50, 23/50, 24/50, 25/50, 26/50, 27/50, 28/50 and 29/50. 

If we want to find some more rational numbers between 22/50 and 23/50, we write 22/50 as 220/500 and 23/50 as 230/500.

Then we get nine rational numbers 221/500, 222/500, 223/500, 224/500, 225/500, 226/500, 227/500, 228/500 and 229/500.

Let us understand this better with the help of the number line in the figure given below. 

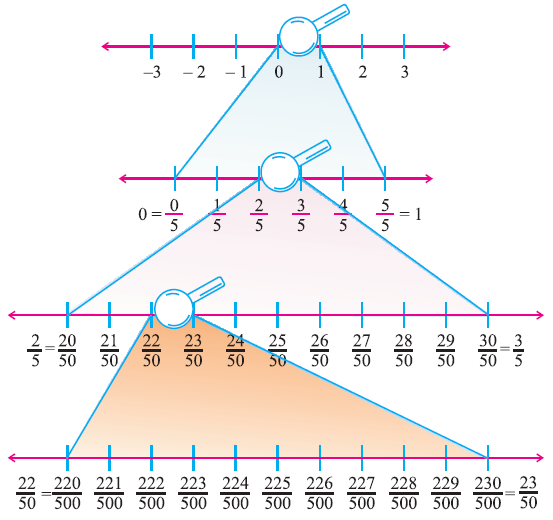
Observe the number line between 0 and 1 using a magnifying lens.

Similarly, we can observe many rational numbers in the intervals 1 to 2, 2 to 3 and so on.

If we proceed like this, we will continue to find more and more rational numbers between any two rational numbers.

This shows that there is high density of rational numbers between any two rational numbers. 

So, unlike natural numbers and integers, there are countless rational numbers between any two given rational numbers.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.