SOLVING SURFACE AREA AND VOLUME PROBLEMS

Problem 1 : 

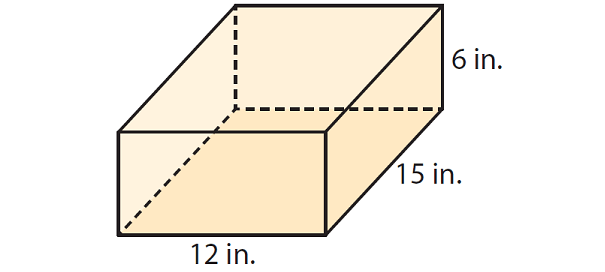
Erin is making a jewelry box of wood in the shape of a rectangular prism. The jewelry box will have the dimensions shown below. The cost of painting the exterior of the box is $0.50 per square in. How much does Erin have to spend to paint the jewelry box ?

Solution : 

To know that total cost of painting, first we have to know the Surface area of the jewelry box. 

Find surface area of the box. 

Step 1 :

Identify a base, and find its area and perimeter.

Any pair of opposite faces can be the bases. For example, we can choose the bottom and top of the box as the bases.

Find base area. 

B  =  l x w

B  =  12 x 15

B  =  180 square in.

Find perimeter of the base. 

P  =  2(12) + 2(15)

P  =  24 + 30

P  =  54 in.

Step 2 : 

Identify the height, and find the surface area.

The height h of the prism is 6 inches. Use the formula to find the surface area.

S  =  Ph + 2B

S  =  54(6) + 2(180)

S  =  684 square inches

Step 3 :

Total cost  =  Area x Cost per square in.

Total cost  =  684 x $0.50

Total cost  =  $342

Hence, Erin has to spend $342 to paint the jewelry box. 

Problem 2 : 

A metal box that is in the shape of rectangular prism has the following dimensions. The length is 9 inches, width is 2 inches, and height is 1 1/2 inches. Find the total cost of silver coating for the entire box. 

Solution : 

To know that total cost of silver coating, first we have to know the Surface area of the metal box. 

Find surface area of the box. 

Step 1 :

Identify a base, and find its area and perimeter.

Any pair of opposite faces can be the bases. For example, we can choose the bottom and top of the box as the bases.

Find base area. 

B  =  l x w

B  =  9 x 2

B  =  18 square in.

Find perimeter of the base. 

P  =  2(9) + 2(2)

P  =  18 + 4

P  =  22 in.

Step 2 : 

Identify the height, and find the surface area.

The height h of the prism is 1 1/2 inches. Use the formula to find the surface area.

S  =  Ph + 2B

S  =  22(1 1/2) + 2(18)

S  =  22(3/2) + 36

S  =  33 + 36

S  =  69 square inches

Step 3 :

Total cost  =  Area x Cost per square in.

Total cost  =  69 x $1.50

Total cost  =  $103.50

Hence, the total cost of silver coating for the entire box is $103.50. 

Problem 3 : 

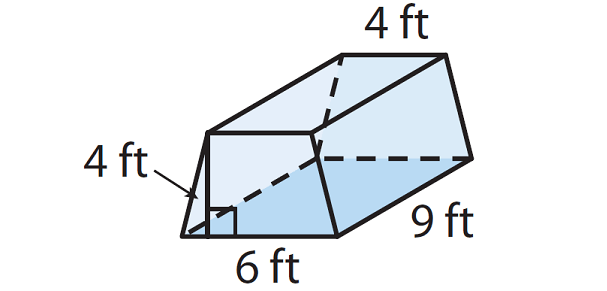
Cherise is setting up her tent. Her tent is in the shape of a trapezoidal prism shown below. How many cubic feet of space are in her tent ?

Solution : 

Step 1 :

To find the number of cubic feet of space in  the tent, we have to find the volume of Cherise's tent. 

Step 2 :

Volume of Cherise's tent (Trapezoidal prism) is 

  =  base area x height

or

V  =  b x h

Step 3 :

Find base area.

Area of trapezoid with bases of lengths b₁ and b₂ and height h. 

Base area (b)  =  (1/2) x (b₁ + b₂)h

Base area (b)  =  (1/2) x (6 + 4)4

Base area  =  20 sq.ft

Step 4 :

Find volume of the prism.

V  =  b x h

V  =  20 x 9

V  =  180 cubic.ft

Hence, the number of cubic feet of space in  Cherise's tent is 180. 

Problem 4 : 

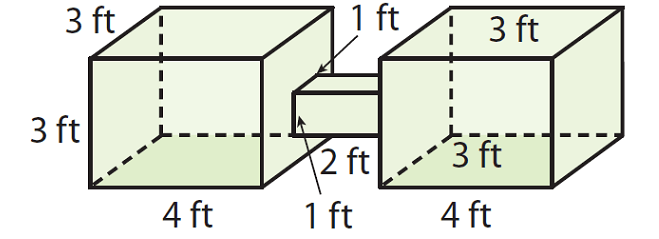
Allie has two aquariums connected by a small square prism. Find the volume of the double aquarium.

Solution : 

Step 1 :

Find the volume of each of the larger aquariums.

Volume  =  Base area x Height

Volume  =  (4 x 3) x 3

Volume  =  12 x 3

Volume  =  36 cubic ft. 

Step 2 :

Find the volume of the connecting prism.

Volume  =  Base area x Height

Volume  =  (2 x 1) x 1

Volume  =  2 x 1

Volume  =  2 cubic ft.

Step 3 :

Add the volumes of the three parts of the aquarium.

V  =  36 + 36 + 2

V  =  74 cubic ft.

The volume of the aquarium is 74 cubic ft.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.