STEPS OF CONSTRUCTION OF CIRCUMCIRCLE

In this section, you will learn how to construct circumcircle.

Circumcircle :

The circle drawn with S (circumcenter) as center and passing through all the three vertices of the triangle is called the circumcircle.

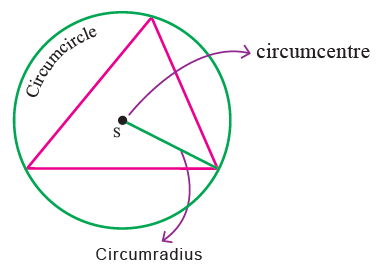
Circumcenter :

The point of concurrency of the perpendicular bisectors of the sides of a triangle is called the circumcenter and is usually denoted by S.

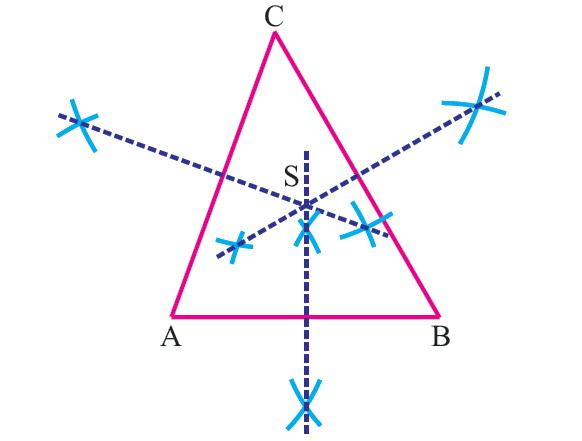
Before we learn how to construct circumcircle of a triangle, first we have to know how to construct perprendicular bisector. 

So, let us learn how to construct perpendicular bisector. 

Construction of Perpendicular Bisector - Steps

To construct a perpendicular bisector, we must need the following instruments.

1. Ruler

2. Compass

The steps for the construction of a perpendicular bisector of a line segment are :

Step 1 :

Draw the line segment AB. 

Step 2 :

With the two end points A and B of the line segment as centers and more than half the length of the line segment as radius draw arcs to intersect on both sides of the line segment at C and D.

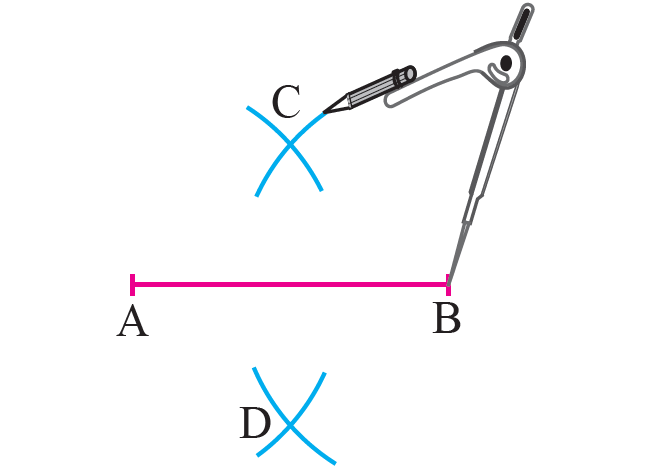
Step 3 :

Join C and D to get the perpendicular bisector of the given line segment AB.

In the above figure, CD is the perpendicular bisector of the line segment AB.

This construction clearly shows how to draw the perpendicular bisector of a given line segment with compass and straightedge or ruler.

This bisects the line segment (That is, dividing it into two equal parts) and also perpendicular to it. 

Now, let us see how to construct the circumcenter and circumcircle of a triangle. 

Constructing Circumcircle - Steps

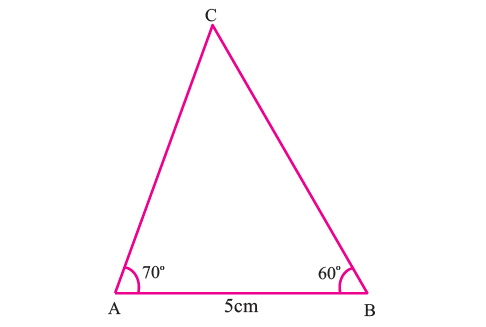
Construct the circumcircle of the triangle ABC with AB = 5 cm, <A = 70° and <B = 50°. And also find the circumradius. 

Step 1 :

Draw triangle ABC with the given measurements.

Step 2 :

Construct the perpendicular bisectors of any two sides (AC and BC) and let them meet at S which is the circumcentre.

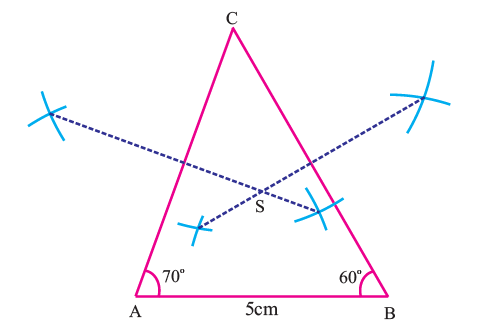
Step 3 :

With S as center and SA = SB = SC as radius, draw the circumcircle to pass through A, B and C.

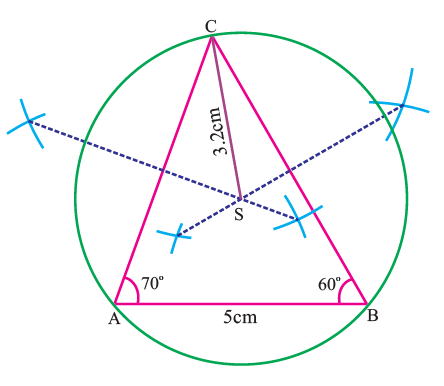
In the above figure, circumradius  =  3.2 cm.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.