SYNTHETIC DIVISION WORKSHEET

Problem 1 :

Find the quotient and remainder when

p(x)  =  3x³ - 2x² - 5 + 7x

is divided by d(x)  =  x + 3. 

Problem 2 :

Find the quotient and remainder :

(x³ + x² - 3 x + 5) ÷ (x - 1)

Problem 3 :

Find the quotient and remainder :

(3x³ - 2x² + 7x - 5) ÷ (x + 3)

Problem 4 :

Find the quotient and remainder :

(3x³ + 4x² - 10x + 6) ÷ (3x - 2)

1. Answer :

(3x³ - 2x² - 5 + 7x) ÷ (x + 3)

Step 1 :

Arrange dividend and the divisor in standard form.

Then, 

3x³ - 2x² + 7x - 5     (standard form of dividend)

x + 3     (standard form of divisor)

Write the coefficients of dividend in the first row.

Put ‘0’ for missing term(s).

3     -2     7     -5     (first row)

Step 2 :

Find out the zero of the divisor.

x + 3  =  0 

x  =  -3

Step 3 : 

Write the zero of divisor in front of dividend in the first row.

Put ‘0’ in the first column of second row.

Step 4 : 

Complete the second row and third row as shown below.

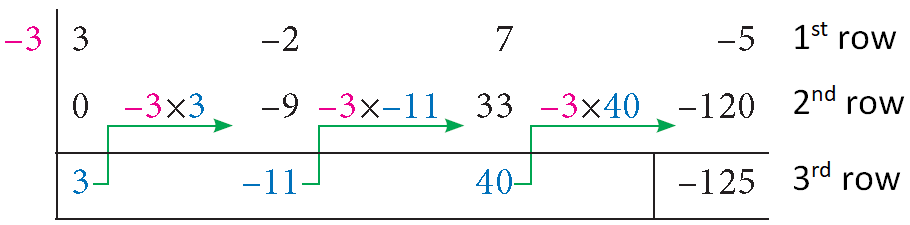
All the entries except the last one in the third row are the coefficients of the quotient.

Therefore, the quotient is

3x² - 11x + 40

and the remainder is

-125

2. Answer :

(x³ + x² - 3 x + 5) ÷ (x - 1)

Arrange dividend and the divisor in standard form.

Then, 

x³ + x² - 3x + 5     (standard form of dividend)

x - 1     (standard form of divisor)

Find out the zero of the divisor.

x - 1  =  0 

x  =  1

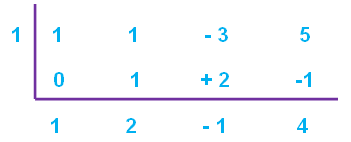
Therefore, the quotient is

x² + 2x - 1

and the remainder is

4

3. Answer :

(3x³ - 2x² + 7x - 5) ÷ (x + 3) 

Arrange dividend and the divisor in standard form.

Then, 

3x³ - 2x² + 7x - 5     (standard form of dividend)

x + 3     (standard form of divisor)

Find out the zero of the divisor.

x + 3  =  0 

x  =  -3

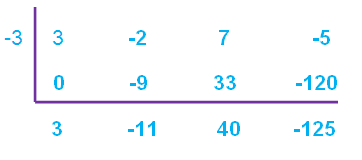
Therefore, the quotient is

3x² - 11x + 40

and the remainder is

-125

4. Answer :

(3x³ + 4x² - 10x + 6) ÷ (3x - 2)

Arrange dividend and the divisor in standard form.

Then, 

3x³ + 4x² - 10x + 6     (standard form of dividend)

3x - 2     (standard form of divisor)

Find out the zero of the divisor.

3x - 2  =  0 

x  =  2/3

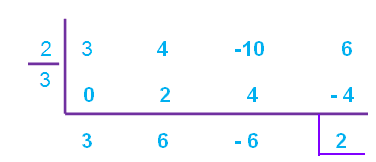
Therefore, the quotient is

3x² + 6x - 6

and the remainder is

2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.