WRITING EQUIVALENT EXPRESSIONS USING DISTRIBUTIVE PROPERTY WORKSHEET
Problem 1 :
Use distributive property to write an expression that is equivalent to 3(10 + 2).
Problem 2 :
Use distributive property to write an expression that is equivalent to 5(6 - 3).
Problem 3 :
Use distributive property to write an expression that is equivalent to 7(x - 3).
Problem 4 :
Use distributive property to write an expression that is equivalent to 2(2x - 5).
Solution :
2(2x - 5) = 2(2x) - 2(5)
2(2x - 5) = 4x - 10
Problem 5 :
Use distributive property to write an expression that is equivalent to 3(x - 5).
Problem 6 :
Use distributive property to write an expression that is equivalent to 5x + 25.
Problem 7 :
Use distributive property to write an expression that is equivalent to 7y + 5y.
Problem 8 :
Use distributive property to write an expression that is equivalent to 0.2y + z.

Detailed Answer Key
Problem 1 :
Use distributive property to write an expression that is equivalent to 3(10 + 2).
Solution :
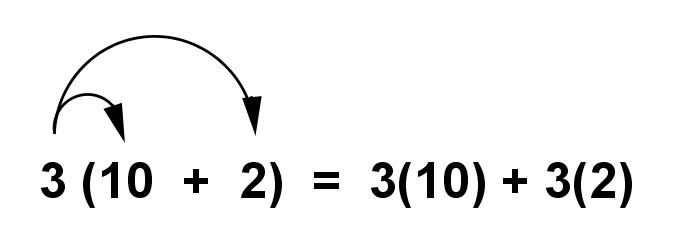
Problem 2 :
Use distributive property to write an expression that is equivalent to 5(6 - 3).
Solution :
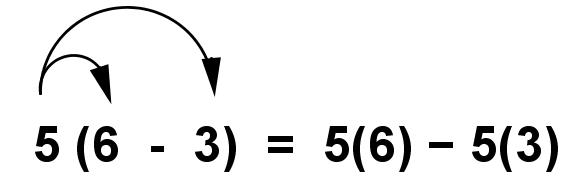
Problem 3 :
Use distributive property to write an expression that is equivalent to 7(x - 3).
Solution :
7(x - 3) = 7x - 7(3)
7(x - 3) = 7x - 21
Problem 4 :
Use distributive property to write an expression that is equivalent to 2(2x - 5).
Solution :
2(2x - 5) = 2(2x) - 2(5)
2(2x - 5) = 4x - 10
Problem 5 :
Use distributive property to write an expression that is equivalent to 3(x - 5).
Solution :
3(x - 5) = 3x - 3(5)
3(x - 5) = 3x - 15
Problem 6 :
Use distributive property to write an expression that is equivalent to 5x + 25.
Solution :
5x + 25 = 5x + 5(5)
5x + 25 = 5(x + 5)
Problem 7 :
Use distributive property to write an expression that is equivalent to 7y + 5y.
Solution :
7y + 5y = y(7 + 5)
Problem 8 :
Use distributive property to write an expression that is equivalent to 0.2y + z.
Solution :
0.2y + z = 0.2y + 1z
0.2y + z = 0.2y + 0.2(5z)
0.2y + z = 0.2(y + 5z)
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Calculus AB Problems with Solutions (Part - 3)
Jan 01, 25 10:53 PM
AP Calculus AB Problems with Solutions (Part - 3) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Dec 30, 24 07:48 PM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 94)
Dec 30, 24 07:47 PM
Digital SAT Math Problems and Solutions (Part - 94)