CROSS PRODUCT RULE IN PROPORTION

Equality of two ratios is called proportion.

a : b = c : d

The two ratios above a : b and c : d are equal. So, they are said to be in proportion. 

The proportion a : b = c : d is read "a is to b as c is to d". The numbers a and d are called the extremes of the proportion. The numbers b and c are called the means of the proportion. 

Cross Product Rule

In a proportion, the product of the extremes is equal to the product of the means. This is called cross product rule.

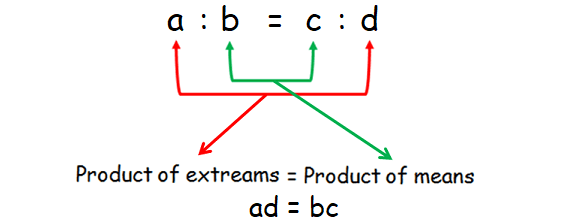
If a/b = c/d, then ad = bc. The products ad and bc are called the cross products of the proportion a/b = c/d.

If three quantities a, b, c are in continuous proportion, then the middle term b is called the mean proportional between a and c, a is the first proportional and c is the third proportional.

Since three quantities a, b, c are in continuous proportion, we can write them as

a : b = b : c

Using cross product rule, we can solve for the mean proportion b.

product of means = product of extremes

b² = ac

Taking square root on both sides,

b = √ac

Solved Problems

Problem 1 :

Check whether the four numbers 2.4, 3.2, 1.5 and 2 are in proportion.

Solution :

In the given numbers,

extremes = 2.4 and 2

means = 3.2 and 1.5

Product of extremes = 2.4 x 2 = 4.8

Product of means = 3.2 x 1.5 = 4.8

4.8 = 4.8

Product of extremes = Product of means

Since, the given numbers satisfy the cross product rule, they are in proportion.

Problem 2 :

Find the fourth proportion to 2/3, 3/7, 4.

Solution :

Let x be the fourth proportion.

Then, we have

2/3 : 3/7 = 4 : x

Using cross product rule,

product of extremes = product of means

(2/3)(x) = (3/7)(4)

2x/3 = 12/7

In the equation above, we have two different denominators 3 and 7.

Least common multiple of (3, 7) = 21.

Multiply both sides of the above equation by 21 to get rid of the denominators.

2x/3 = 12/7

21(2x/3) = 21(12/7)

7(2x) = 3(12)

14x = 36

Divide both sides by 14.

x = 36/14

x = 18/7

The fourth proportion is 18/7.

Problem 3 :

Find the third proportion to 2.4 and 9.6.

Solution :

Let x be the third proportion. Then, the numbers are

2.4, 9.6, x

Proportion :

2.4 : 9.6 = 9.6 : x

Using cross product rule,

product of extremes = product of means

2.4x = (9.6)(9.6)

2.4x = 92.16

Divide both sides by 2.4.

x = 38.4

The third proportion is 38.4.

Problem 4 :

Find the mean proportion between 1.25 and 1.8.

Solution :

Let x be the mean proportion. Then, the numbers are

1.25, x, 1.8

Proportion :

1.25 : x = x : 1.8

Using cross product rule,

product of means = product of extremes

(x)(x) = (1.25)(1.8)

x² = 2.25

Take square root on both sides.

√x² = √2.25

x = 1.5

The mean proportion is 1.5.

Example 5 :

Carter’s SUV requires 8 gallons of gasoline to travel 148 miles. How much gasoline, to the nearest gallon, will he need for a 888 mile trip?

Solution :

Let x be the no. of gallons of gasoline required for a 888 mile trip.

Form the proportion with the given information.

x gallons : 888 miles = 8 gallons : 148 miles

x : 888 = 8 : 148

Using cross product rule,

148x = (888)(8)

148x = 7104

Divide both sides by 148.

x = 48

So, 48 gallons of gasoline required for a 888 miles trip.

Example 6 :

If Andy drove 84 miles in 1 hour 45 minutes, how many miles can he drive in 5 hours?

Solution :

Let x be the no. of miles driven by Andy in 5 hours.

1 hours 45 minutes = 1⁴⁵⁄₆₀ hours

= 1¾ hours

= 7/4 hours

Form the proportion with the given information.

x miles : 5 hours = 84 miles : 1 hour 45 minutes

x miles : 5 hours = 84 miles : 7/4 hours

x : 5 = 84 : 7/4

Using cross product rule,

(7/4)x = (5)(84)

7x/4 = 420

Multiply both sides by 4.

7x = 1680

Divide both sides by 7.

x = 240

Andy can drive 240 miles in 5 hours.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.