10th GRADE MATH PRACTICE QUESTIONS WITH SOLUTION

Problem 1 :

Find the number of integers between 60 and 600 which are divisible by 9.

Solution :

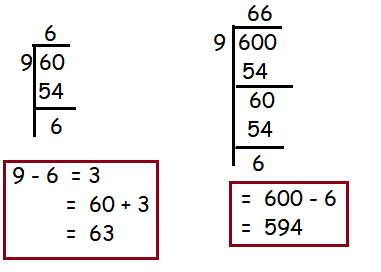
Terms which are divisible by 9 between 60 and 600.

63, 72, 81, ........ 594

n  =  [ (l - a)/d ] + 1

n  =  [(594 - 63)/9] + 1

n  =  (531/9) + 1

n  =  59 + 1

n  =  60

So, the number of terms divisible by 9 between 60 and 600 is 60.

Problem 2 :

The sum of a two digit number and the number obtained by reversing the digits is 66. If the digits of the number differs by 2, find the number.

Solution :

Let xy be the required two digit number.

xy + yx  =  66

10x + y + 10y + x  =  66

11x + 11y  =  66

Dividing it by 11, we get

x + y  =  6 -----(1)

x - y  =  2 -----(2)

(1) + (2)

2x  =  8

x  =  4

By applying the value of x in (2), we get

4 - y  =  2

y  =  4 - 2

y  =  2

So the required two digit number is 42.

Problem 3 :

Find two consecutive odd positive integers, sum of their squares is 290.

Solution :

Let x and x + 2 are two consecutive numbers.

x² + (x + 2)²  =  290

x² + x² + 4x + 4  =  290

2x² + 4x - 286  =  0

Dividing the entire equation by 2, we get

x² + 2x - 143  =  0

(x + 13) (x - 11)  =  0

x  =  -13 or x  =  11

So, the two consecutive odd numbers are 11 and 13.

Problem 4 :

A boy of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/s.The lamp is 3.6 m above the ground level, find the length of her shadow after 4 seconds.

Solution :

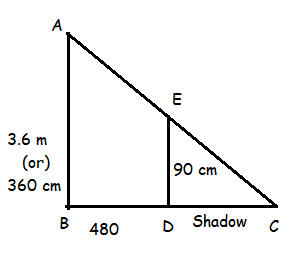
Two triangles, ABC and EDC are similar.

AB/DE  =  BD/DC

360 / 90  =  (480 + DC) / DC

4 DC  =  480 + DC

3DC  =  480

DC  =  160

DC  =  1.6 m

So, the length of shadow after 4 seconds is 1.6 m.

Problem 5 :

If the points A (4, 6), B(10, 4), C(8, 2) and D(b, 4) are the vertices of a parallelogram taken in order, find the value of b.

Solution :

Midpoint of diagonal AC  =  Midpoint of diagonal BD

Midpoint  =  (x₁ + x₂)/2, (y₁ + y₂)/2

(4 + 8)/2, (6 + 2)/2  =  (10+b)/2, (4 + 4)/2

12/2, 8/2  =  (10+b)/2, 8/2

(6, 4)  =  ((10+b)/2, 4)

Equating x coordinates,

6  =  (10 + b)/2

12  =  10 + b

b  =  12 - 10

b  =  2

So, the value of b is 2.

Problem 6 :

A circus artist is climbing a 20 m long rope, which is stretched and tied from the top of a vertical pole to the ground.Calculate the height of the pole, if the angle  created  by the rope with the ground level is 30°.

Solution :

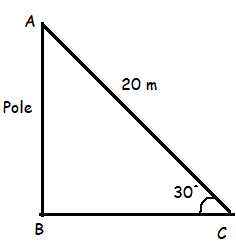
AB - height of pole, AC - length of rope, BC - horizontal distance between pole and the point C.

sin θ  =  AB/AC

sin 30  =  AB/20

1/2  =  AB/20

AB  =  20/2

AB  =  10

So, height of the pole is 10 m.

Problem 7 :

A farmer wishes to start a 100 sq.m rectangular garden. Since he has only 30 m barbed wire, he fences the sides of a rectangular garden getting letting his house compound wall act as the fourth side fence. Determine the dimension of the garden.

Solution :

Area of rectangular garden  =  100 sq.m

Let x be the length and y be the width of the rectangular wall.

Quantity of wire to be used for fencing  =  30 m

2x + y  =  30

y  =  30 - 2x  -----(1)

xy  =  100 ----(2)

x(30 - 2x)  =  100

30x - 2x²  =  100

Divide it by 5, we get

x² - 15x + 50  =  0 

(x - 10) (x - 5)  =  0

x - 10  =  0  and x - 5  =  0

x  =  10 and x  =  5

Problem 8 :

Find the area of the shaded portion in the below figure, where ABCD is a square of side 14 cm.

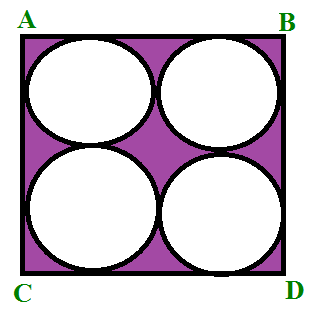
Solution :

Side length of square is 14 cm.

Diameter of each circle  =  7 cm

radius  =  7/2

Area of circle  =  πr²

  =  (22/7) ⋅ (7/2)²

Area of 4 circles  =  4 ⋅ (22/7) ⋅ (7/2)²

=  154

Area of square  =  14²  =  196

Area of shaded region  =  196 - 154

  =  42 cm²

Area of the shaded region is 42 cm².

Problem 9 :

Find the centroid of the triangle whose vertices are the points (8, 4) (1, 3) and (3, -1).

Solution :

Centroid of the triangle 

=  (x₁+x₂+x₃)/3, (y₁+y₂+y₃)/3

=  (8+1+3)/3, (4+3-1)/3

=  12/3, 6/3

=  (4, 2)

So, centroid of the given triangle is (4, 2).

Problem 10 :

The standard deviation and the mean of 20 values are 21.2 and 36.6.Find the coefficient of variation.

Solution :

Standard deviation (σ)  =  21.2

Mean (x̅) =  36.6

Coefficient of variation  =  (σ/x̅) ⋅ 100%

  =  (21.2/36.6) ⋅ 100%

  =  0.579 ⋅ 100%

  =  57.9

So, the coefficient of variation is 57.9.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.