PEMDAS RULE

PEMDAS is the rule that can be used to simplify or evaluate complicated numerical expressions with more than one binary operation.

Very simply way to remember PEMDAS rule!

P ----> Parentheses

E ----> Exponent 

M ----> Multiply

D ----> Divide

A ----> Add

S ----> Subtract

Important Notes :

1. In the simplification of a particular numerical expression, if both multiplication and division are there, do the operations one by one in the order from left to right.

2. Always multiplication can not be expected before division. Do one by one in the order from left to right.

3. In the simplification of a particular numerical expression, if both addition and subtraction are there, do the operations one by one in the order from left to right.

Examples :

18 ÷ 9 x 5 = 2 x 5 = 10

20 - 5 + 7 = 15 + 7 = 22 

In the simplification of the two numerical expressions above, we have both division and multiplication. From left to right, division comes first and multiplication comes next. So, do division first and multiplication next.

Problem 1 :

Evaluate :

12 + 4 x 3.25

Solution :

Multiply ----> = 12 + 4 x 3.25

Add ----> = 12 + 13

Answer ----> = 25

Problem 2 :

Evaluate :

35 ÷ 7 + 2² 

Solution :

Exponent ----> = 35 ÷ 7 + 2²

Divide ----> = 35 ÷ 7 + 4

Add ----> = 5 + 4

Answer ----> = 9

Problem 3 :

Evaluate :

2.5 x (13 - 5)

Solution :

Parentheses ----> = 2.5 x (13 - 5)

Multiply ----> = 2.5 x 8

Answer ----> = 20

Problem 4 :

Evaluate :

45 ÷ (6 + 3) x 3 - 6 ÷ 2

Solution :

Parentheses ----> = 45 ÷ (6 + 3) x 3 - 6 ÷ 2

Divide ----> = 45 ÷ 9 x 3 - 6 ÷ 2

Multiply ----> = 5 x 3 - 6 ÷ 2

Divide ----> = 15 - 6 ÷ 2

Subtract ----> = 15 - 3

Answer ----> = 12

Problem 5 :

Evaluate :

48 - 3(16 + 15 ÷ 5 x 3 - 2 x 3) + 8

Solution :

Parentheses ----> = 48 - 3(16 + 15 ÷ 5 x 3 - 2 x 3) + 8

Divide ----> = 48 - 3(16 + 15 ÷ 5 x 3 - 2 x 3) + 8

Multiply ----> = 48 - 3(16 + 3 x 3 - 2 x 3) + 8

Multiply ----> = 48 - 3(16 + 9 - 2 x 3) + 8

Add ----> = 48 - 3(16 + 9 - 6) + 8

Parentheses ----> = 48 - 3(25 - 6) + 8

Multiply ----> = 48 - 3(19) + 8

Subtract ----> = 48 - 57 + 8

Subtract ----> = -9 + 8

Answer ----> = -1

Problem 6 :

Evaluate :

7 + [(25 - 1) ÷ (3² - 3)] - 3

Solution :

Brackets ----> = 7 + [(25 - 1) ÷ (3² - 3)] - 3

Parentheses ----> = 7 + [(25 - 1) ÷ (3² - 3)] - 3

Exponent ----> = 7 + [24 ÷ (3² - 3)] - 3

Brackets ----> = 7 + [24 ÷ 6] - 3

Add ----> = 7 + 4 - 3

Subtract ---> = 11 - 3

Answer ----> 8

Problem 7 :

Evaluate :

(63 ÷ 7) + 22 x (9 + 1) ÷ 11

Solution :

Parentheses = (63 ÷ 7) + 22 x (9 + 1) ÷ 11

Parentheses ----> = 9 + 22 x (9 + 1) ÷ 11

Multiply ----> = 9 + 22 x 10 ÷ 11

Divide ----> = 9 + 220 ÷ 11

Add ----> = 9 + 20

Answer ----> = 29

Problem 8 :

Evaluate :

(146 - 2) ÷ (3 x 4) - 15 + 9

Solution :

Parentheses ----> = (146 - 2) ÷ (3 x 4) - 15 + 9

Parentheses ----> = 144 ÷ (3 x 4) - 15 + 9

Divide ----> = 144 ÷ 12 - 15 + 9

Subtract ----> =  12 - 15 + 9

Subtract ----> = -3 + 9

Answer ----> = 6

Problem 9 :

Evaluate :

78 ÷ 13 + (24 - 12) x 5

Solution :

Parentheses ----> = 78 ÷ 13 + (24 - 12) x 5

Divide ----> = 78 ÷ 13 + 12 x 5

Multiply ----> = 6 + 12 x 5

Add ----> = 6 + 60

Answer ----> = 66

Problem 10 :

Evaluate :

(24 + 1) x 2 ÷ (13 - 3) - 19

Solution :

Parentheses ----> = (24 + 1) x 2 ÷ (13 - 3) - 19

Parentheses ----> = 25 x 2 ÷ (13 - 3) - 19

Multiply ----> = 25 x 2 ÷ 10 - 19

Divide ----> = 50 ÷ 10 - 19

Subtract ----> = 5 - 19

Answer ----> = -14

Problem 11 :

Evaluate :

[12 - 36 ÷ (4² - 4) ÷ 3 + 2] x 5

Solution :

Brackets ----> = [12 - 36 ÷ (4² - 4) ÷ 3 + 2] x 5

Parentheses ----> = [12 - 36 ÷ (4² - 4) ÷ 3 + 2] x 5

Exponent ----> = [12 - 36 ÷ (4² - 4) ÷ 3 + 2] x 5

Parentheses ----> = [12 - 36 ÷ (16 - 4) ÷ 3 + 2] x 5

Divide ----> = [12 - 36 ÷ 12 ÷ 3 + 2] x 5

Divide ----> = [12 - 3 ÷ 3 + 2] x 5

Subtract ----> = [12 - 1 + 2] x 5

Add ----> = [11 + 2] x 5

Multiply ----> = 13 x 5

Answer ----> = 65

Problem 12 :

Evaluate :

a³ - (b² + c)² ÷ a + (bc + a)

if a = 4, b = -3 and c = 7.

Solution :

a³ - (b² + c)² ÷ a³ + (bc + a)

Substitute a = 4, b = -3 and c = 7.

4³ - ([(-3)² + 7)² ÷ 4³ + [(-4)7 +7]

Evaluation :

Brackets ----> = 4³ - [(-3)² + 7]² ÷ 4³ + [(-4)7 + 7]

Exponent ----> = 4³ - [(-3)² + 7]² ÷ 4³ + [(-4)7 + 7]

Brackets ----> = 4³ - [9 + 7]² ÷ 4³ + [(-4)7 + 7]3

Brackets ----> = 4³ - 16² ÷ 4³ + [(-4)7 + 7]

Multiply ----> = 4³ - 16² ÷ 4³ + [(-4)7 + 7]

Brackets ----> = 4³ - 16² ÷ 4³ + [-28 + 7]

Exponent ----> = 4³ - 16² ÷ 4³ + [-21]

Exponent ----> = 64 - 16² ÷ 4³ + [-21]

Exponent ----> = 64 - 256 ÷ 4³ + [-21]

Divide ----> = 64 - 256 ÷ 64 + [-21]

Multiply ----> = 64 - 4 + [-21]

Subtract ----> = 64 - 4 - 21

Subtract ----> = 60 - 21

Answer ----> = 39

Problem 13 :

Evaluate the following expression for x = -1 and y = 2 :

x² + 3y³

Solution :

= x² + 3y³

Substitute x = -1 and y = 2.

= (-1)² + 3(2)²

Evaluation :

Exponent ----> = (-1)² + 3(2)²

Exponent ----> = 1 + 3(2)²

Multiply ----> = 1 + 3(4)

Add ----> = 1 + 12

Answer ----> 13

Problem 14 :

Evaluate the following expression for x = 1 and y = 1.

(y³ + x) ÷ 2 + x

Solution :

= (y³ + x) ÷ 2 + x

Substitute x = 1 and y = 1.

= (1³ + 1) ÷ 2 + 1

Evaluation :

Parentheses ----> = (1³ + 1) ÷ 2 + 1

Exponent ----> = (1³ + 1) ÷ 2 + 1

Parentheses ----> = (1 + 1) ÷ 2 + 1

Divide ----> = 2 ÷ 2 + 1

Add ----> = 1 + 1

Answer ----> = 2

Problem 15 :

Evaluate the following expression for y = 3 and z = 7.

z³ - (y ÷ 3 - 1)

Solution :

= z³ - (y ÷ 3 - 1)

Substitute y = 3 and z = 7.

= 7³ - (3 ÷ 3 - 1)

Evaluation :

Parentheses ----> = 7³ - (3 ÷ 3 - 1)

Divide ----> = 7³ - (3 ÷ 3 - 1)

Parentheses = 7³ - (1 - 1)

Exponent ----> = 7³ - 0

Answer ----> = 243

Problem 16 :

Evaluate :

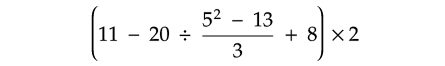
Solution :

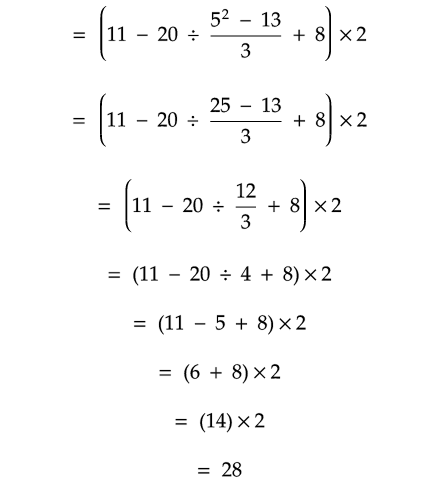
Problem 17 :

What is the value of

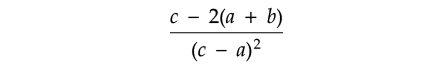
if a = -1/2, b = 3/2 and c = 5/2?

Solution :

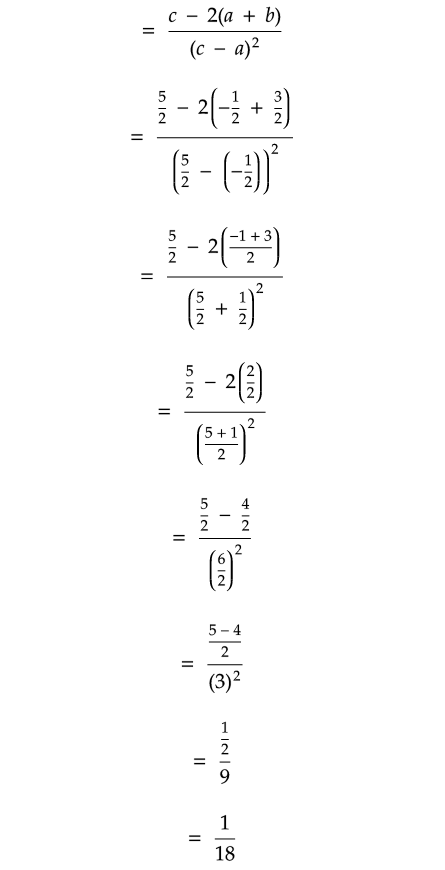
Problem 18 :

What is the value of

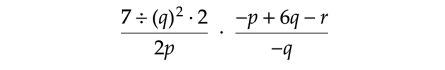
if p = 4, q = 1/2 and r = 2?

Solution :

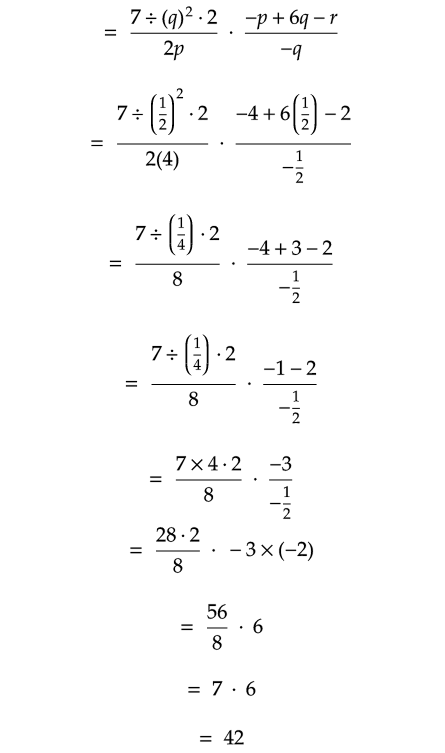
Click here to get step by step answers for the above questions.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.