COMPOUND ANGLES FORMULAS

Now, compound angles are algebraic sum of two or more angles. Trigonometric functions do not satisfy the functional relations like

f(x + y) = f(x) + f(y) and f(kx) = kf(x), k is a real number

For example,

cos(α + β) ≠ cosα + cosβ, sin2α ≠ 2sinα, tan3β ≠ 3tanβ

Thus we need to derive formulas for

sin(α + β), cos(α + β), tan(α + β)

and use them in calculations of application problems.

Formula 1 : cos(α + β) = cosαcosβ - sinαsinβ

Proof :

Consider the unit circle with center at O. Let P = P(1, 0).

Let Q, R and S be points on the unit circle such that

∠POQ = α, ∠POR = α + β and ∠POS = -β

as shown in the figure shown below.

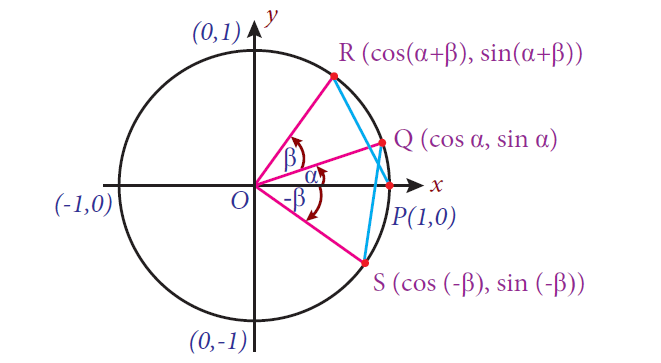
Clearly angles α, α + β and -β are in standard positions. Now, the points Q, R and S are given by

Q(cosα, sinα)

R(cos(α + β), sin(α + β))

S(cos(-β), sin(-β))

ΔPOR and ΔSOQ are congruent.

So, PR = SQ which gives PR² = SQ².

Thus, [cos(α + β) - 1]² + sin²(α + β) :

= [cosα - cos(-β)]² + [sinα - sin(-β)]² - 2cos(α + β) + 2

= 2 - 2cosαcosβ + 2sinαsinβ

Hence,

cos(α + β) = cosαcosβ - sinαsinβ

Note :

(i) In the above proof, PR = SQ says that the distance between two points on a circle is determined by the radius and the central angle.

(ii) Arcs PR and SQ subtend angles α + β and α + (-β) respectively at the center. Thus PR = SQ. Thus, distance between the points (cosα, sinα) and (cos(-β), sin(-β)) is same as the distance between the points

(cos(α + β), sin(α + β)) and (1, 0)

(iii), In the above derivations, 0 ≤ α ≤ 2π, 0 ≤ β ≤ 2π. Because of periodicity of sine and cosine, the result follows for any α and β.

Formula 2 : cos(α - β) = cosαcosβ + sinαsinβ

Proof :

We know that cos(α + β) = cosα cosβ - sinα sinβ

Now,

cos(α - β) = cos[α + (-β)]

= cosαcos(-β) - sinαsin(-β)

Hence,

cos(α - β) = cosαcosβ + sinαsinβ

Note :

(i) If α = β, the above formula is reduced to

cos²α + sin²α = 1

(i) If α = 0 and β = x, then cos(-x) = cosx, which shows that cosx is an even function.

Formula 3 : sin(α + β) = sinαcosβ + cosαsinβ

Proof :

This formula may be proved by writing

sin(α + β) = cos[π/2 - (α + β)]

= cos[(π/2 - α) - β]

Using Formula 2,

= cos(π/2 - α)cosβ + sin(π/2 - α)sinβ

Hence,

sin(α + β) = sinαcosβ + cosαsinβ

Note :

If α + β = π/2, the above identity is reduced to

cos²α + sin²α = 1

Formula 4 : sin(α - β) = sinαcosβ - cosαsinβ

Proof :

This formula may be proved by writing

sin(α - β) = sin[α + (-β)]

Using Formula 3,

= sinαcos(-β) + cosαsin(-β)

Hence,

sin(α - β) = sinαcosβ - cosαsinβ

Formula 5 : tan(α + β) = (tanα + tanβ)/(1 - tanαtanβ)

Proof :

tan(α + β) = sin(α + β)/cos(α + β)

= (sinαcosβ + cosαsinβ)/(cosαcosβ - sinαsinβ)

Dividing both numerator and denominator by cosαcosβ,

tan(α + β) = (tanα + tanβ)/(1 - tanαtanβ)

Formula 6 : tan(α - β) = (tanα - tanβ)/(1 + tanαtanβ)

Proof :

tan(α + β) = tan[(α + (-β)]

Using Formula 5,

= [tanα + tan(-β)]/[(1 - tanαtan(-β)]

tan(α + β) = (tanα - tanβ)/(1 + tanαtanβ)

Trigonometric Ratio Table

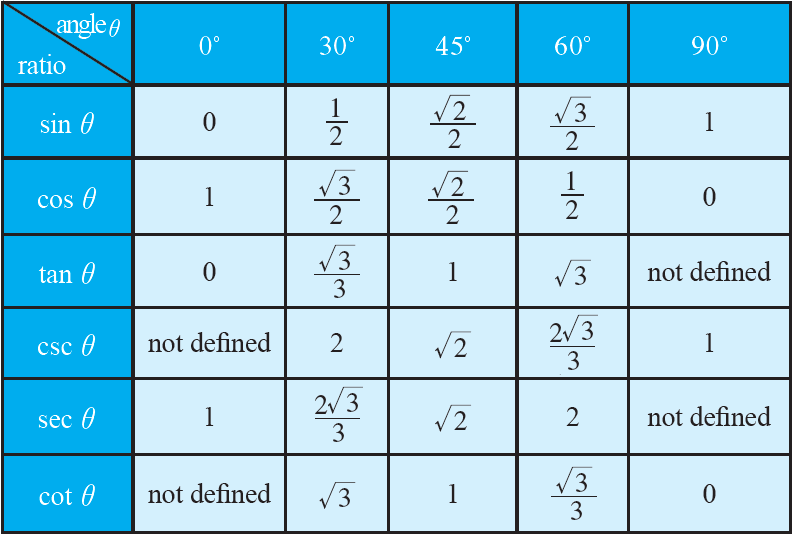
From the above table, we can get the values of trigonometric ratios for standard angles such as 0°, 30°, 45°, 60°, 90°.

Solved Problems

Problem 1 :

Find the value of cos15°.

Solution :

Write the given angle 15° in terms of sum or difference of two standard angles.

15° = 45° - 30°

cos15° = cos(45° - 30°)

= cos45°cos30° + sin45°sin30°

Using the above trigonometric ratio table, we have

= (√2/2) ⋅ (√3/2) + (√2/2) ⋅ (1/2)

= (√6/4)  +  (√2/4)

= (√6 + √2)/4

Problem 2 :

Find the value of sin75°.

Solution :

Write the given angle 75° in terms of  sum or difference of two standard angles.

75° = 45° + 30°

sin75° = sin(45° + 30°)

sin75° = sin45°cos30° + cos45°sin30°

Using the above trigonometric ratio table, we have

= (√2/2) ⋅ (√3/2) + (√2/2) ⋅ (1/2)

= (√6/4) + (√2/4)

= (√6 + √2)/4

Problem 3 :

Find the value of tan15°.

Solution :

Write the given angle 15° in terms of  sum or difference of two standard angles.

15° = 45° - 30°

tan15° = tan(45° - 30°)

tan15° = (tan45° -  tan30°)/(1 + tan45°tan30°)

Using the above trigonometric ratio table, we have

= (1 - 1/√3)/(1 + 1 ⋅ 1/√3)

=  (1 - 1/√3)/(1 + 1/√3)

= (√3/√3 - 1/√3)/(√3/√3 + 1/√3)

= [(√3 - 1)/√3]/[(√3 + 1)/√3]

= [(√3 - 1)/√3] x [(√3/(√3 + 1)]

= (√3 - 1)/(√3 + 1)

By rationalizing the denominator, we get

= 2 - √3

Problem 4 :

Find the value of tan165°.

Solution :

Write the given angle 165° in terms of  sum or difference of two standard angles.

165° = 120° + 45°

tan165° = tan(120° + 45°)

tan165° = (tan120° + tan45°)/(1 - tan120°tan45°) ----(1)

tan120° = tan(180° - 60°) = -tan60° = -√3.

(1)----> = (-√3 + 1)/[1 - (-√3)(1)]

= (1 - √3)/(1 + √3)

Problem 5 :

If sinA = 4/5 (in quadrant I) and cosB = -12/13 (in quadrant II), then find (i) sin(A - B), (i) cos(A- B).

Solution :

sin²A + cos²A = 1

cos²A = 1 - sin²A

cosA = ±√(1 - sin²A)

Substitute sinA = 4/5.

cosA = ±√[1 - (4/5)²]

= ±√[1 - 16/25]

= ±√[(25 - 16)/25]

= ±√(9/25)

= ± 3/5

In the first quadrant, cosA is always positive.

cosA = 3/5

And also,

sin²B + cos²B = 1

sin²B = 1 - cos²B

sinB = ±√(1 - cos²B)

Substitute cosB = -12/13.

sinB = ±√[1 - (-12/13)²]

= ±√[1 - 144/169]

= ±√[(169 - 144)/169]

= ±√[25/169]

= ± 5/13

In the second quadrant sinB is always positive.

sinB = 5/13

sin(A - B) :

= sinAcosB - cosAsinB

= (4/5)(-12/13) - (3/5)(5/13)

= -48/65 - 15/65

sin(A- B) = -63/65

cos(A - B) :

= cosAcosB + sinAsinB

= (3/5)(-12/13) + (4/5)(5/13)

= -36/65 + 20/65

cos(A- B) = -16/65

Problem 6 :

If sinA = 3/5 and cosB = 9/41 , 0 < A < π/2, 0 < B < π/2, find the value of (i) sin(A + B) (ii) cos(A − B).

Solution :

sin(A + B) :

= sinAcosB + cosAsinB

 = (3/5)(9/41) + (4/15)(40/41)

= (27/205) + (160/205)

= (27 + 160)/205

= 187/205

cos(A - B) :

= cosAcosB + sinAsinB

= (4/5)(9/41) + (3/5)(40/41)

= (36/205) + (120/205)

= (36 + 120)/205

= 156/205

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.