10TH GRADE MATH WORKSHEET WITH ANSWERS

Problem 1 :

A rubber ball dropped from a height of 50 m rebounds at every impact from the floor to a height half of that from which is has fallen. Find the distance described by the time it comes to rest.

Solution :

Distance described in the 1^st impact  =  50 m

Distance described in the 2^nd impact  =  25

Distance described in the 3^rd impact  =  25/2

Distance described in the 4^rth impact  =  25/4

Distance described by the time it comes to rest

  =  50 + [25 + (25/2) + (25/4) + ............]

Sum of infinite geometric series = a/(1 - r)

a  =  25    r  =  t₂/t₁  ==>  1/2

S_∞  =  a/(1 - r)

  =  25/(1/2)

  =  50

Distance described by the time it comes to rest

  =  50 + 2(50) 

  =  50 + 100

  =  150

So, the correct answer for this question is 150 m.

Problem 2 :

A work was assigned to me on a Tuesday. I completed to work after 72 days. On what day, i completed the work.

Solution :

Tuesday corresponds to 2 in the clock.

Then, 2 + 72  =  74

When we divide 74 by 7, we get 4 as remainder.

4 corresponds to Thursday.

So, i completed the work on Thursday.

Problem 3 :

The radius of the top of a bucket is 18 cm and that of the bottom is 6 cm.Its depth is 24 cm. Determine the capacity of the bucket.

Solution :

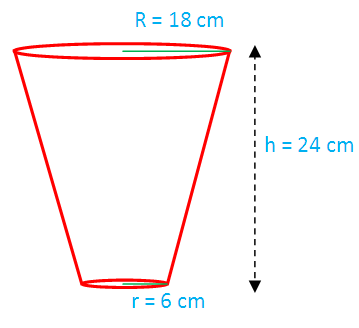
Volume of frustum cone  =  (1/3) π h (R² + r ² + R r)

  =  (1/3) π (24) (18² + 6 ² + (18)(6))

  =  8π(324 + 36 + 108)

  =  8π(468)

  =  3744 π cm³

So, the correct answer is 3744 π cm³

Problem 4 :

A solid metal cylinder is 20 cm in height and has a radius of 1.5 cm. This is melted down and cast into spheres each of radius 1.5 cm.How many spheres each of radius 1.5 cm can be cast from the cylinder ?

Solution :

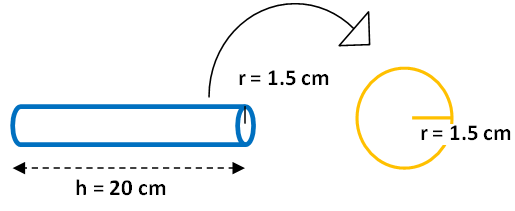
Height of the cylinder(h)  =  20 cm

Radius of cylinder ( R)  =  1.5 cm

Radius of sphere (r)  =  1.5 cm

Volume of cylinder  =  n ⋅ Volume of sphere

π R² h  =  n x (4/3) ⋅ π r³

(1.5)² ⋅ 20  =  n ⋅ (4/3) ⋅ (1.5)³

(1/1.5) ⋅ (3/4) ⋅ 20  =  n

n  =  (1/1.5) ⋅ 3 ⋅ 5

n  =  (5/0.5)

n  =  10

Problem 5 :

In a higher secondary class, 66 play football,56 play hockey, 63 play cricket, 27 play both foot ball and hockey, 25 play hockey and cricket, 23 play cricket and foot ball and 5 do not play any game. if the strength of the class is 130. Calculate the number who play all the three games.

Solution :

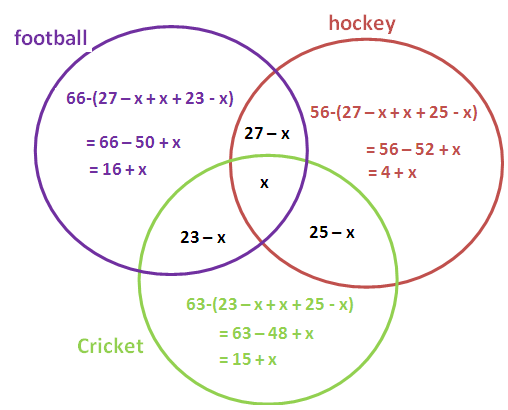
Let A, B and C be the number of students who play foot ball, hockey and cricket respectively.

Number of students who play foot ball  =  66

Number of students who play hockey  =  56

Number of students who play cricket  =  63

Number of students who play football and hockey  =  27

Number of students who play hockey and cricket  =  25

Number of students who play cricket and football  =  23

Number of students who do not play any game  =  5

Let x be the number of students who play all the three game.

Number of students who play any one of the games  =

16+x+27-x+x+23-x+25-x+4+x+15+x

125  =  16 + 27 + 23 + 25 + 4 + 15 + x

x  =  125 - 110

x  =  15

Number of students who play all the three games  =  15.

Problem 6 :

Determine the value of m if x+1 is a factor of

x³ + mx² + 19x + 12

Solution :

Let p(x)  =  x³ + mx² + 19 x + 12

x + 1  =  0

x  =  -1

Since(x + 1) is a factor p(-1)  =  0

p(-1)  =  (-1)³ + m (-1)² + 19 (-1) + 12

0  =  -1 + m - 19 + 12

0  =  -20 + 12 + m

0  =  -8 + m

m  =  8

So, the value of m is 8.

Problem 7 :

Find the square root of

(x² - 4) (x² + x - 6) (x² + 5x + 6)

Solution :

  =  √(x² - 4) (x² + x - 6) (x² + 5 x + 6)

  =  √(x² - 2²) (x + 3) (x - 2) (x + 2)(x + 3)

  =  √(x + 2) (x - 2)(x + 3) (x - 2) (x + 2)(x + 3)

  =  (x + 2) (x - 2)(x + 3)

So the correct answer is (x + 2) (x - 2)(x + 3).

Problem 8 :

The outer dimension of a bordered table are 72 cm and 108 cm. If the area of a table, excluding the border is 6400 cm², how wide is the border ?

Solution :

Let x be the width of the border.

Outer length of table  =  108 cm

Width of the table  =  72 cm

Area of the table including the border

  =  108(72) - (108-2x)(72-2x)

6400  =  108(72) - [108(72) - 108(2x) - 2x(72) + 2x²)]

6400  =  108(72) - 108(72) - 216x - 144x + 2x²

2x² - 360x  =  6400

x² - 180x - 3200  =  0

(x - 160) (x - 20)  =  0

x  =  160 and x  =  20

Problem 9 :

Find the area of the triangle whose vertices are

(4, 5) (4, 2) (-2, 2).

Solution :

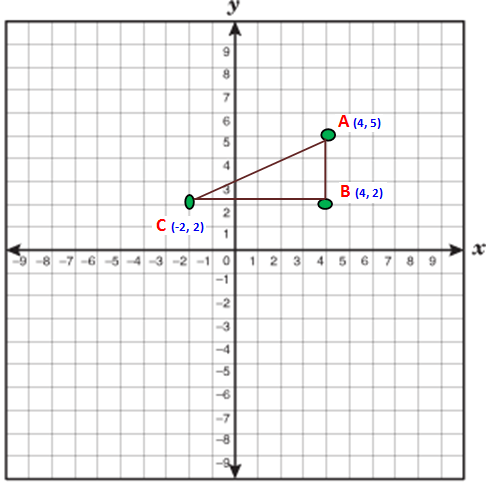
Now we should take anticlockwise direction. So, we have to take the points in the following order.

A (4, 5) C (-2, 2) and B (4, 2)

Area of the triangle 

=  (1/2) [x₁(y₂-y₃) + x₂(y₃-y₁) + x₃(y₁-y₂)]

x₁  =  4 x₂  =  -2 x₃  =  4

y₁  =  5 y₂  =  2 y₃  =  2

Area of the triangle ACB

  =  1/2 [4(2-2) + (-2)(2-5) + 4(5-2)]

  =  1/2 [(-2)(-3) + 4(3)]

  =  1/2 {0 + 6 + 12}

  =  18/2

  =  9 square units

So, required area of the triangle is 9 square units.

Problem 10 :

Find the equation of the straight line which joins the points A (5,1) and B (-2,2)

Solution :

Equation of the line joining two points

(y - y₁)/(y₂ - y₁) = (x - x₁)/(x₂ - x₁)

x₁  =  5, x₂  =  -2, y₁  =  1 and y₂  =  2

(y - 1)/(2 - 1)  =  (x - 5)/(-2 - 5)

(y - 1)/1  =  (x - 5)/(-7)

-7 (y - 1)  =  1 (x - 5)

-7 y + 7  =  x - 5

 x + 7 y - 5 - 7  =  0

x + 7 y - 12  =  0

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.