6TH GRADE MATH QUIZ WITH ANSWERS

Question 1 :

Fill in the boxes.

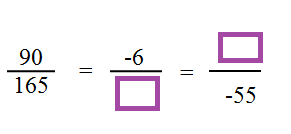
 (A) -2 & -15        (B) -11 & -30     (C) -30 & -11

Solution :

Let x be the denominator of the second fraction.

Since they are equivalent fractions 

90/(-6)  =  -15

90/(-15)  =  -6

165/(-15)  =  -11

So, the second fraction is

-6/(-11)

If we multiply the denominator of the second fraction by 5, we will get -55, that is the denominator of the third fraction.

So, the numerator also be multiplied by 5 to get the numerator of the third fraction.

Question 2 :

A car travels 432 km on 48 liters of petrol. How far would it  travel on 20 liters of petrol?

(A) 180 km     (B) 130 km     (C) 152 km

Solution :

432 km   ------->  48 liters 

x km  ----> 20 liters 

It is in direct variation

432 ⋅ 20  =  48 ⋅ x

x  =  (432 ⋅ 20)/48

x  =  180

So, the car can travel 180 km for 20 liters of petrol.

Question 3 :

An electric pole, 24 meters high casts a shadow of 20 meters. Find the height of a tree. If it casts a shadow of 15 meters under similar conditions

 (A) 15 m         (B) 17 m          (C) 18 m

Solution :

Now we need to find the length of the tree when it casts a shadow of 15 meters.

Since it is direct variation,

24 ⋅ 15  =  x ⋅ 20

360  =  20 x

360/20  =  x

x  =  18 m

So the correct answer is 18 m

Question 4 :

A train 315 m long is running at 54 km/h.How much time will it take to cross a pole?

(A) 15 seconds      (B) 21 seconds    (C) 30 seconds

Solution :

Now, we are going to use the formula to find time

Time  =  Distance/Speed

Length of the train  =  distance covered by the train 

=  315 m

Speed of the train  =  54 km/hr

To convert the speed from km/hr to m/second we have to multiply by 5/18

  =  54 ⋅ (5/18)

  =  15 m/sec

Time  =  315/15

=  21 seconds

So, the correct answer is 21 seconds.

Question 5 :

In an examination John secured 372 marks. If she secured 62% marks, find the maximum marks.

(A) 500      (B) 600     (C) 700

Solution :

Marks secured by John  =  372

Let x be the maximum marks

62% of x  =  372

(62/100) ⋅ x  =  372

x  =  372 ⋅ (100/62)

x  =  37200/62

x  =  600

So,the maximum mark is 600.

Question 6 :

Length of a rectangle is 8 m less than twice its breadth. If the perimeter of the rectangle is 56 m, find the length and breadth.

(A) 16 m & 12 m    (B) 16 m & 11 m     (C) 12 m & 16 m

Solution :

Let x be the breadth of the rectangle

So,length of the rectangle  =  2x - 8

Perimeter of the rectangle  =  56 m

Perimeter of a rectangle  =  2 (length + breadth)

2(2x - 8 + x)  =  56

2 (3x - 8)  =  56

6x - 16  =  56

6 x  =  56 + 16

6 x  =  72

x  =  72/6

x  =  12

breadth of the rectangle  =  12 m

length of the rectangle  =  2(12) - 8

  =  24 - 8

  =  16 m

So, the answer is 12 m & 16 m.

Question 7 :

Factorize  9m² - 12mn  + 4n²

(A) (3m+2n) (3m+2n)     (B) (3m+2n) (3m-2n)

(C) (3m-2n) (3m-2n)

Solution :

  =  3²m² - 2(6mn) + 2²n²

  =  (3 m)² - 2 (3m)(2n) + (2n)²

This exactly matches the algebraic identity

a² - 2ab + b²

So, we shall written it as (3 m - 2 n)²

Therefore the factors are (3m - 2n) (3m - 2n)

Question 8 :

The length of the sides of a right triangle are 6 cm and 8 cm. What is the length of its hypotenuse ?

(A) 6 cm     (B) 10 cm    (C) 5 cm

Solution :

In a right triangle, the square of hypotenuse side is equal to the sum of squares of other two sides.

(Hypotenuse)²  =  6² + 8²

Hypotenuse  =  √(36 + 64)

Hypotenuse  =  √100

Hypotenuse  =  10

Question 9 :

A rectangular lawn of length 40 m and breadth 25 m is to be surrounded externally by a path which is 2 m wide. Find the area of the path.

 (A) 266 m²         (B) 255 m²        (C) 276 m²

Solution :

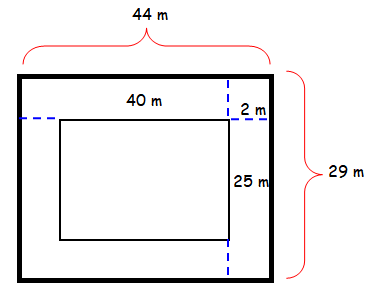
Area of path

  =  Area of large rectangle - area of small rectangle

Area of a rectangle  =  Length x breadth

  =  (44 x 29) - (40 x 25)

  =  1276 - 1000

  =  276 m²

So, the answer is 276 m².

Question 10 :

Capacity of a tank is 60 m³. If the length and breadth of the tank are 5 m and 4 m respectively, find its depth.

(A) 3 m      (B) 5 m     (C) 7 m

Solution :

Capacity of the tank  =  60 m³

length  =  5 m, breadth  =  4 m and height  =  ?

Capacity of the tank  =  length ⋅ breadth ⋅ height 

  60  =  5 ⋅ 4 ⋅ h

h  =  60/20

h  =  3

So, the height of the tank is 3 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.