8TH GRADE MATH QUIZ

Question 1 :

Find the value of x in

x : 7 :: 2 : 10.

(A) 1.4        (B) 3.7        (C) 2.8

Solution :

Since the given are in proportion, 

Product of mean  =  Product of median

x(10)  =  7(2)

 x  =  14/10

  x  =  1.4

Question 2 :

A fort had enough food for 120 soldiers for 200 days. After 5 days 30 soldiers leave the fort. How long will the remaining food last now ?

(A) 120 days         (B) 150 days         (C) 100 days

Solution :

Consider 1 person consumes x food per day

120 persons = 120 x

Total available food  =  200 ⋅ 120 ⋅ x  = 24000x

Food consumed in 5 days = 5 ⋅ 120 ⋅ x = 600x

Food available =  total food - food consumed in 5days

  =  24000x - 600x

  =  23400x

5 days later 30 soldiers left and there will be 90 soldiers be there.

Food consumed by 90 people for 1 day  =  90x

No of days food will last  =  food available/ food consumed per 1 day

  =  23400x /90x

  =  260 days

Question 3 :

If a scooter travels 155 km on 5 liters of petrol, how many kilometers will it travel on 9 liters of petrol ?

(A) 139 km         (B) 279 km          (C) 100 km

Solution :

Using 5 liters of petrol, we can travel 155 km. Form this let us find how far we can travel using 1 liter of petrol.

5 liters  =  155

1 liter  =  155/5

1 liter  =  31 km

9 liters  =  31(9)

9 liters  =  279 km

So, he can travel 279 km using 9 liters of petrol.

Question 4 :

Given that the area of square is 81 cm². The perimeter of the square.

(A)  36 cm      (B)  49 cm    (C)  64 cm

Solution :

Area of the square  =  81 cm²

a²  =  81

a  =  9

Perimeter of the square  =  4a

  =  4(9)

  =  36 cm

Question 5 :

ABCD is a parallelogram in which angle of DAB and DBC 75°, 60° respectively. Calculate the angles CDB and ADB.

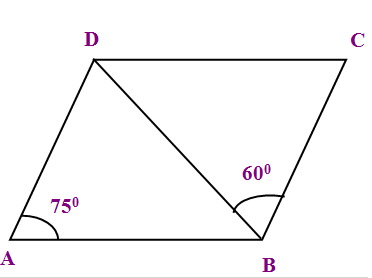
(A)  49°, 51°       (B)  45°, 60°         (C)  21°,75°

Solution :

In a parallelogram the opposite angles are equal.

<DCB  =  75

In triangle CDB,

<CDB + <DBC + <BCD  =  180

<CDB + 60 + 75  =  180

<CDB  =  180 - 135

<CDB  =  45

Because it is a parallelogram, the sides AB and CD are parallel and DB is the transversal.

<BDC  =  <DBA

<DBA  =  45

In triangle ADB,

<ADB + <ABD + <BAD  =  180

<ADB + 45 + 75  =  180

<ADB  =  180 - 120

<ADB  =  60

So, the required angles are 45 and 60 respectively.

Question 6 :

If the selling price of 10 articles is equal to the cost price of 11 articles. Find the profit percent.

(A) 15%        (B) 10%      (C) 12%

Solution :

Selling price of 10 articles  =  Cost price of 11 articles

Let 1 be the cost price of 1 article.

Cost price of 11 articles  =  $11

Selling price of 10 articles  =  $10

Cost price of 10 articles  =  $10

Profit %  =  ((11 - 10) / 10)⋅100%

Profit %   =  (1/10)⋅100%

Profit %  =  10%

Question 7 :

Find AC when AB  =  15 cm, AD  =  10 cm, AE  =  8 cm

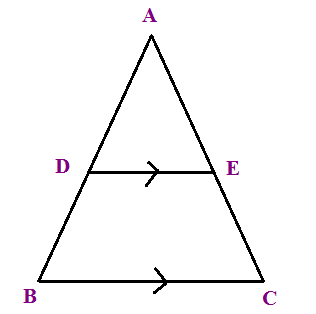
(A)  2 cm        (B)  8 cm    (C)   4 cm

Solution :

AB  =  15

AD + BD  =  15

10 + BD  =  15

BD  =  5

In triangle ABC, the sides DE and BC are parallel.

AD/DB  =  AE/EC

10/5  =  8/EC

2  =  8/EC

EC  =  8/2

EC  =  4 cm

Question 8 :

Angle ABC measures 250°, find the measure of minor of arc ACB.

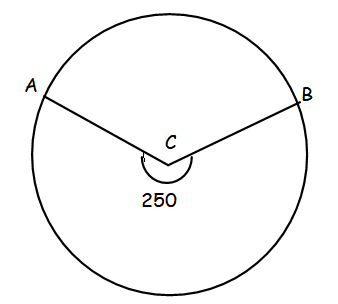
(A)  150°       (B)  110°        (C)  140°

Solution :

Given that :

Reflexive angle of ACB  =  250

Measure of minor arc of ACB  =  360 - 250

  =  110°

So, the required angle measure is 110°.

Question 9 :

Find the mean of all odd numbers between 80 and 88.

(A) 84          (B) 30       (C) 62

Solution :

First, let us list out the odd numbers between 80 and 88.

81, 83, 85 and 87

Mean  =  (81 + 83 + 85 + 87)/4

=  336/4

=  84

So, the required mean is 84.

Question 10 :

The number of times a particular observation occur in a data is called its __________

(A) Frequency     (B) Mean       (C) Median

Solution :

The number of times a particular observation occur in a data is called its frequency.

Answer Key

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.