8th GRADE MATH WORKSHEET WITH EXPLANATIONS

Question 1 :

Ronald has wondered that who else participates in math team, physics team, and choir. There are 300 people who participate in at least one of the three activities, 150 who participate in choir, 200 who participate in math team, 32 who participate in physics team, 70 who participate in both choir and math team, 12 who participate in both choir and physics team, and 8 who participate in both math team and physics team. How many people participate in all three activities?

(A) 8         (B) 15          (C) 10

Solution :

Number of people people who participate atleast one of the game  =  300

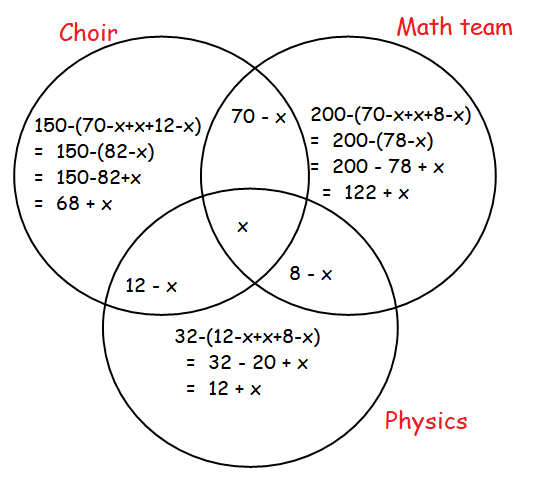
Number of people who participate atleast one of the game  

  =  68 + x + 70 - x + 122 + x + x + 12 - x + 8 - x + 12 + x

  =  292 + x

292 + x  =  300

 x  =  300 - 292

x  =  8

So, the number of students who participate in all three activities is 8.

Question 2 :

If 2^x  =  2⁴, then the value of x is

(A) 2       (B) 4         (C) 10

Solution :

2^x  =  2⁴

Since the bases are equal, we can equate the powers.

x  =  4

Question 3 :

Ali bought a bamboo pole of length 200 cm. He first painted 30% of the length of the pole with red paint. Then, he painted 50% of the unpainted portion of the pole with green paint. What was the length (in cm) the unpainted portion ?

(A) 100 cm       (B) 40 cm         (C) 70 cm

Solution :

Length of the pole painted using red  =  30% of 200

  =  60

Part of pole unpainted  =  200 - 60

=  140

Length of the pole painted using green  =  50% of 140

=  70

The remaining 50% is unpainted. So, the answer is 70 cm.

Question 4 :

The amount of money David has is 1/4 of the amount of money Samuel has. If Samuel gives David $500, Samuel will have 2/3 of the money David has. How much money do they have altogether ?

Solution :

Let x be the amount that Samuel has 

Amount that David has  =  1/4 of x

After given 500 to David

Samuel has  =  x - 500 and David has (x/4) + 500

(x - 500)  =  (2/3) of [(x/4) + 500]

3(x - 500)  =  2[(x/4) + 500]

3x - 1500  =  2x/4 + 1000

3x - x/2  =  1000 + 1500

5x/2  =  2500

x  =  2500(2/5)

x  =  1000 (Samuel)

David has  =  1/4 of 1000  =  250

Altogether  =  1000 + 250

So, they had 1250.

Question 5 : 

At a wedding dinner, all the men wear pants. 1/4 of the number of women wear pants while the rest of the women wear dresses. If the number of women is 2/3 of the number of men, what percentage of the people at the wedding wear dresses ?

Solution :

Let x be the total number of men

Number of women  =  2/3 of x

  =  2x/3

Total number of participants  =  x + 2x/3

=  5x/3

Number of women who wear pants  =  1/4 of (2x/3)

  =  x/6

Number of women who wear dresses  =  (2x/3) - (x/6)

  =  x/6

Percentage of women who wear dresses

  =  [(x/6) / (5x/3)] ⋅ 100

=  (x/6) ⋅ (3/5x) ⋅ 100

=  30%

Question 5 :

Kevin plays darts on a circular dartboard that is made up of two concentric circles (two circles with the same center but different sizes). Getting a bulls-eye means hitting anywhere in the inner circle, which has radius 2 inches. The outer circle has radius 3 inches. Kevin always hits the dartboard, but does not always get a bulls-eye. If Kevin has an equal chance of hitting each point on the dartboard, what is the probability that Kevin gets a bulls-eye in his next shot ?

(A) 2/9        (B) 4/9        (C) 1/2

Solution :

Area of the card board  =  n(S)

Radius of outer circle (R) =  3 inches

Radius of inner circle (r)  =  2 inches

=  π(2)²/π(3)²

=  4/9

Question 6 :

On a test, Rose was asked to add 9 to a number x, and then divide the result by 2. However, Rose accidentally subtracted 9 from x and then multiplied the result by 2. Luckily for her, she still got the correct answer ! Find x.

(A) 12        (B) 15        (C) 10

Solution :

(9 + x)/2  =  2(x - 9)

9 + x  =  4(x - 9)

9 + x  =  4x - 36

9 + 36  =  4x - x

3x  =  45

x  =  15

Question 7 :

If 3x + 3x  =  432, find x.

(A) 72     (B) 50      (C) 21

Solution :

3x + 3x  =  432  

6x  =  432

x  =  72

So the value of x is 72.

Question 8 :

In a circle, the length of the line which is passing from one end of the circle to another end of the circle through the center is 14. What is the perimeter of the circle ?

(A) 14         (B) 44           (C) 16

Solution :

The line which connects the end points of the circle drawn through the center is known as diameter.

Diameter  =  14

Radius  =  7

Perimeter of circle  =  2πr

  =  2⋅(22/7)⋅7

  =  44

Question 9 :

In a figure given below, the shaded region BCFG is a square. If GE  =  18 cm and AC  =  24 cm, what is the perimeter (in cm) of the rectangle ADEH

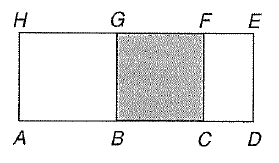
Solution :

AC  =  HF  =  24, BD  =  GE  =  18

AC + BD + EG + HF  =  24 + 18 + 18 + 24

  =  84

AC  =  AB + BC, BD  =  BC + CD

AC + BD  =  AB + BC + BC + CD

We can replace one BC by CF and CF can be replaced by ED.

So,

AC + BD  =  AB + BC + ED + CD  ---(1)

EG + HF  =  EF + FG + FG + HG

We can replace one FG by GB and GB can be replaced by HA.

So,

EG + HF  =  EF + FG + HA + HG  ---(2)

(1) + (2)

AC + BD + EG + HF  =  AB + BC + ED + CD + EF + FG + HA + HG 

84  =  Perimeter of rectangle

Question 10 :

A teacher raises chickens and rabbits in his classroom. He counts 450 total animals, and 1050 total legs on the animals. Each chicken has 2 legs, while each rabbit has 4 legs. How many rabbits does the teacher have ?

(A) 75       (B) 50       (C) 38

Solution :

Let x and y be the total number of chickens and rabbits the teacher has.

x + y  =  450  ---(1)

2x + 4y  =  1050  ---(2)

(1) ⋅ 4 ==>  4x + 4y  =  1800

                2x + 4y  =  1050

                (-)     (-)     (-)

             --------------------

               2x  =  750

x  =  750/2

x  =  375

By applying the value of x in (1), we get

375 + y  =  450

y  =  450 - 375

y  =  75

So, the number of rabbits are 75.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.