PSAT MATH PRACTICE QUESTIONS

Question 1 :

What is the least possible value of (x² - 1)/x, if x ≥ 1

(A)  -1  (B)  0  (C)  3  (D)  3/4  (E)  2/3

Solution :

To find the least possible value of (x² - 1)/x, we have to simplify

(x² - 1)/x  =  (x + 1)(x - 1)/x

Since the value of x is  greater than or equal to 1, we may apply x = 1.

  =  (1 + 1) (1 - 1)/2

  =  0/2

  =  0

Hence the least possible value for x is 0.

Question 2 :

What is the maximum number of points in which a circle and triangle can intersect ?

(A)  3  (B)  5  (C)  6  (D)  8  (E)  ∞

Solution :

Let us draw a circle and triangle to intersect each other at maximum points.

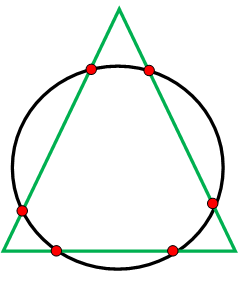
From the picture, there are 6 points can intersect both circle and triangle.

Question 3 :

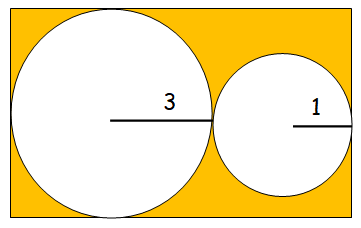
What is the area of the shaded region ?

(A)  48 - 10π  (B)  64 - 22π  (C)  10π 

(D)  48 - 6π  (E)  16π

Solution :

In order to find the area of shaded region, we have to subtract the areas of two circles from the area of rectangle.

Area of circle  =  πr²

Radius of larger circle  =  3, radius of small circle  =  1

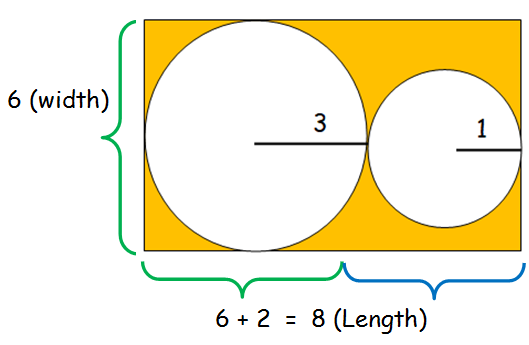
Area of shaded region 

  =  Area of rectangle - Areas of circles

  =  length ⋅ width - [π(3)² + π(1)²]

  =  8 ⋅ 6 - π [9 + 1]

  =  48 - 10π

Question 4 :

There are 45 plastic ducks in a bag. If there are black, green, blue and purple plastic ducks and 1/3 of the plastic ducks are black, 1/5 of the plastic ducks are blue, one third of the number of black plastic ducks are green, then how many purple plastic ducks are in the bag ?

(A)  6  (B)  15  (C)  16  (D)  21  (E)  39

Solution :

There are 4 colors of plastic ducks, black, green, blue and purple.

Number of black ducks  =  (1/3) of 45  =  15

Number of blue ducks  =  (1/5) of 45  =  9

Number of green ducks  =  (1/3) of 15  =  5

Number of purple ducks  =  45 - (15 + 9 + 5)  

  =  45 - 29

  =  16

Hence the number of purple ducks is 16.

Question 5 :

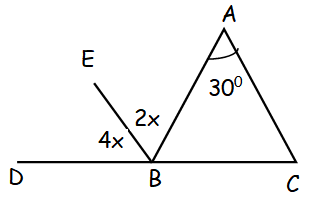
In the figure above, point B is on the line segment DC. If AB  =  BC, what is the measure of the angle ABE ?

(A)  20°  (B)  40°  (C)  80°  (D)  90°  (E)  100°

Solution :

Since AB and BC are equal, it forms same angle.

<ABC  =  180 - (<BAC + <BCA)

  =  180 - (30 + 30)

  =  180 - 60

  =  120

<DBE + <EBA + <ABC  =  180

4x + 2x + 120  =  180

6x  =  180 - 120

6x  =  60  ==>  x  =  10

2x  =  2(10)  =  20° 

Question 6 :

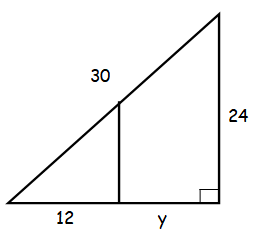
According to the figure above, what is the value of y ?

(A)  3  (B)  6  (C)  12  (D)  15  (E)  18

Solution :

Since it is right triangle, we may apply the concept Pythagorean theorem.

30²  =  24² + (12+y)²

900  =  576 + (144 + 24y + y²)

900  =  720 + 24y + y²

y² + 24y + 720 - 900  =  0 

y² + 24y - 180 = 0 

y² + 30y - 6y - 180 = 0 

y(y + 30) - 6(y + 30)  =  0

(y - 6) (y + 30)  =  0

 y  =  6 (or) y = -30

The negative values is not possible. Hence the value of y is 6.

Question 7 :

A painter needs 4 gallons of paint to paint each room. If a house has 8 rooms in total, how many quarts of paint is he going to need ?

(A)  12  (B)  32  (C)  128  (D)  200 (E)  512

Solution :

A painter needs 4 gallons of paint to paint each room.

Number of gallons of points needed to paint 8 rooms 

  =  8(4)

  =  32 gallons

1 gallon  =  4 quats

Number of quats of paint needed to paint  =  32 (4)  =  128 quats. 

Question 8 :

A rectangle is inscribed in a circle. The rectangle is tangent at the points A, B, C and D. If the diagonal of the rectangle is 20 inches long. What is the area of the circle ?

(A)  10π  (B)  15π  (C)  20π  (D)  100π  (E)  400π

Solution :

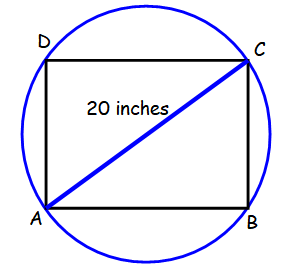
AC is the diameter of the circle, then radius of the circle

  =  10 inches

Area of circle  =  πr²

  =  π(10)²

  =  100π

Question 9 :

The prices in the table given below  show the different types of gas offered at a gas station and the prices of gas per gallon. If Emily has $50, what is the least amount of gas, in gallons, she can purchase subtracted from the greatest amount of gas, in gallons, she can purchase ?

(A)  2  gallons  (B)  3 gallons  (C)  5 gallons  

(D)  20 gallons  (E)  25 gallons

Solution :

Number of gallons of gas filled by choosing unloaded gas 

=  50/2.50

=  20 gallons

Number of gallons of gas filled by choosing regular gas 

=  50/2

=  25 gallons

=  25 - 20 

Required number of gallons  =  5 gallons

Question 10 :

3[9 ÷ (-3)]  + [-3 - (-8)]  =

(A)  -20  (B)  -4  (C)  -2  (D)  2  (E)  14 

Solution :

  =  3[9 ÷ (-3)]  + [-3 - (-8)]

  =  3(-3)  + (-3 + 8)

  =  -9  + 5

  =  -4

Hence the answer is -4.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.