PSAT MATH PRACTICE QUIZ

Question 1 :

Evaluate [(1/2)-(3/4)] ÷ (1/2)  = 

(A)  1/2  (B)  3/2  (C)  -1/2  (D)  -3/4  (E)  1

Solution :

=   [(1/2)-(3/4)] ÷ (1/2)

  =  [(2 - 3)/4] ÷ (1/2)

  =  (-1/4)  ÷ (1/2)

  =  (-1/4) ⋅ (2/1)

=  -1/2

Hence the answer is -1/2.

Question 2 :

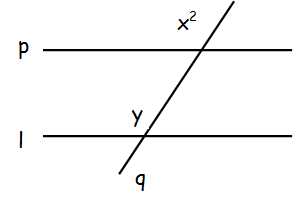
Line q intersects the parallel lines p and l. What is y³/3 ?

(A)  x⁴/3  (B)  x⁶  (C)  x⁹  (D)  x⁴/9  (E)  x⁶/3

Solution :

The lines p and l are parallel lines and q is a transversal. So, corresponding angle are equal.

y = x²

 y³/3  =  (x²)³/3

=  x⁶/3

Hence the value y³/3 is x⁶/3.

Question 3 :

Given the arithmetic sequence x, y, 30, z, f then find x + y + z + f.

(A)  60  (B)  80  (C)  120  (D)  130  (E)  140

Solution :

In a arithmetic sequence, the common difference is d. Each consecutive terms differs by d. The values of x,y, z and f in terms of the difference d, is 

x  =  30 - 2d

y  =  30 - d

z  =  30 + d

f  =  30 + 2d

x + y + z + f  =  30 - 2f + 30 - d + 30 + d + 30 + 2d

  =  120

Hence the answer is 120.

Question 4 :

If (-1)²  =  1, then the value (-1) ²⁰²³ is

(A)  -2023  (B)  -1  (C)  0  (D)  1  (E)  2023

Solution :

(-1) ²⁰²³  =  (-1)²⁰²² ⋅ (-1)

  =  ((-1)²)¹⁰¹¹ ⋅ (-1)

  =  1¹⁰¹¹ ⋅ (-1)

  =  1¹⁰¹¹ ⋅ (-1)  =  -1

Hence the answer is -1.

Question 5 :

Caroline has two times as many marbles as Jake. Jake has 12 less than 7 times as many marbles James has. James has 14 marbles. How many marbles dies Caroline have ?

(A)  52  (B)  54  (C)  86  (D)  98  (E)  172

Solution :

Number of marbles with James  =  14

Number of marbles with Jake  =  7(14) - 12

  =  98 - 12

  =  86

Number of marbles with Caroline  =  2 (86)

  =  172

Hence Caroline has 172 marbles.

Question 6 :

John is trying to escape a ditch. Every time he jumps 10 meters, he falls back 5 meters right after. The ditch is 19 meters long. What is the minimum number of jumps he needs to make to escape ?

(A)    (B)  4  (C)  5  (D)  7  (E)  8

Solution :

At the first jump, he reaches 10 meters, but he falls back 5 meters. Now, John crossed 5 m.

At the second jump, he reaches from 5 m to 15 m, but he falls back 5 m. So, he will be at 10 m.

At the third jump, he reaches from 10 m to 20 m, but he falls back 5 m. So, he will be at 15 m

At the fourth jump, he reaches from 15 m to 25 m, but he falls back 5 m. So, he will be at 20 m

So, 4 jumps are required to escape a ditch of length 19 m.

Question 7 :

What is the largest number of digits the product of 3 digit and 2 digit number has ?

(A)  4  digit  (B)  5 digit  (C)  6 digit 

(D)  7 digit  (E)  8 digit

Solution :

The product of 3 digit and 2 digit number will be 4 digit  or 5 digit number.

Since we need the largest number of digits, the answer is 5 digits.

Question 8 :

 If Fn  =  2 F_n-1 + 3 F_n-2, then what is F₃ if F₁  =  F₂  =  1 ?

(A)  2  (B)  3  (C)  4  (D)  5  (E)  10

Solution :

n = 3

F₃  =  2 F_3-1 + 3 F_3-2

F₃  =  2 F₂ + 3 F₁

F₃  =  2 (1) + 3 (1)

F₃  =  2 + 3  =  5

Question 9 :

Sam walks 3 m to the west, then 4m south, then 4 m North. How far is he from his original location?

(A)  3 m (B)  5 m (C)  7 m  (D)  8 m  (E)  12 m

Solution :

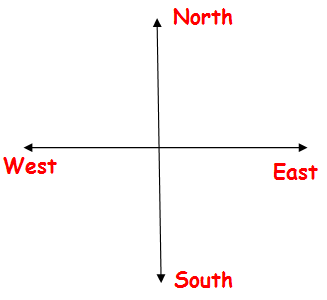
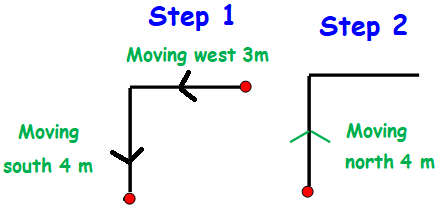
So he will be at 3 m distance from the starting point.

Question 10 :

If a = 3 and b = 5, what is the value of 9a/(b-a) ?

(A)  9  (B)  27  (C)  13/5  (D)  27/2  (E)  26/5

Solution :

9a / (b - a)  =  9(3)/(5-3)

  =  27/2

Hence the answer is 27/2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.