SHSAT MATH PRACTICE TEST QUESTIONS

Question 1 :

Thirty of the fifty students who took an exam received a grade of 90%  or greater.  What percentage of those fifty students received a grade of less than 90%?

(A)  70  (B)  35  (C)  40  (D)  30  (E)  10

Solution :

Total number of students  =  50

Number of students scored 90% or

more than 90% marks   =  30

Percentage of students who score

more than 90% of marks  =  (30/50) ⋅ 100%

  =  60%

So, 60% of students are scoring 90% or more than 90% of marks.

Hence 40% students are getting lesser than 90% marks.

Question 2 :

Let n be a number from -3 to 4 inclusive.  What is the range of values of n²?

(A)  -9 ≤ n² ≤ 16  (B)   9 ≤ n² ≤ 16  (C)  3 ≤ n² ≤ 4 

(D)  0 ≤ n² ≤ 2  (E)  0 ≤ n² ≤ 16

Solution :

The range of n² lies between 9 to 16 (inclusive).

Question 3 :

A is 3 times C.  B is 8 less than C.  For what value of C does A = B?

(A)  -4  (B)  0  (C)  1  (D)  2  (E)  5/2

Solution :

Given that :

A  =  3 C

B  =  C - 8

A  =  B

3 C   =  C - 8

3C - C  =  -8

2C  =  -8

C  =  -4

Hence the answer is -4.

Question 4 :

In a class of 28 students, everyone likes math, English, or both.  If 17 like math and 19 like English, how many like both?

 (A)  2  (B)  8  (C)  16  (D)  20  (E)  28

Solution :

Number of students in a class  =  28

Number of students who like math  =  17

Number of students who like English  =  19

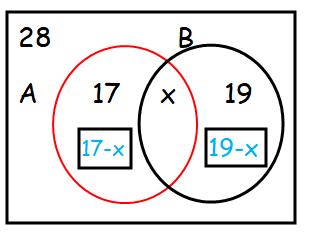
Number of students who like at least one  =  28

17 - x + x + 19 - x  =  28

36 + x  =  28

x  =  28 - 36

x  =  8

Hence the number of students who like both subject is 8.

Question 5 :

Let x = 3²·5³·7⁴ and y = 2³·3·5².  What is the greatest common factor of and y?

(A)  2· 3 · 5 · 7  (B)  2³ · 3² · 5³ · 7⁴  (C)  3 · 5 

(D)  3 · 5²  (E)  3²·5³

Solution :

x = 3²·5³·7⁴ and y = 2³·3·5²

Common factors are 3 · 5².

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.