SHSAT MATH PRACTICE

Question 1 :

If 3x + 2y = 19 and 2x + 3y = 91, what is the value of x + y ?

(A) 8 (B) 9 (C) 21 (D) 22 (E) 72

Solution :

In order to solve these equations, we may use elimination method.

3x + 2y = 19 -------(1)

2x + 3y = 91 -------(2)

(1) ⋅ 3 ==> 9x + 6y = 57

(1) ⋅ 2 ==> 4x + 6y = 182

(-) (-) (-)

------------------

5x = -125

x = -125/5 = -25

By applying x = -25 in (1), we get

3(-25) + 2y = 19

-75 + 2y = 19

2y = 19 + 75

2y = 94

y = 94/2 = 47

x + y = -25 + 47 = 22

Hence the value of x + y is 22.

Question 2 :

Kenny buys candy bars at 9 for $1 and sells them at 3 for $1. How many candy bars must he sell in order to make a profit of exactly $10.

(A) 27 (B) 30 (C) 45 (D) 60 (E) 90

Solution :

Let x be the number of candies that he has to sell to make the profit of $10.

Cost price of 9 candy bars = $1

Cost price of 1 candy = 1/9

Cost price of x candy bars = x/9

Selling price of 3 candy bars = $1

Selling price of 1 candy = 1/3

Selling price of x candy bars = x/3

Profit = Selling price - Cost price

10 = (x/3) - (x/9)

10 = (3x - x)/9

90 = 2x

x = 45

Hence he has to sell 45 candies to make the profit of $10.

Question 3 :

Juan travels at the rate of 30 miles per hour for 4 hours. He then returns over the same route in 3 hours. What was his average rate for the return trip, in mile per hour ?

(A) 22 1/2 (B) 34 2/7 (C) 35 (D) 36 (E) 40

Solution :

Speed = 30 miles per hour

Time taken for travelling = 4 hours

Time = Distance / speed

4 = Distance/30

Distance = 30(4) = 120 miles

Now, we have to find the speed taken by him to cover the the same distance that is 120 miles in 3 hours.

3 = 120/Speed

Average speed = 120/3 = 40 miles per hour

Question 4 :

The value of 3⁵ + 3⁵+ 3⁵ is

(A) 3⁶ (B) 3¹⁵ (C) 9⁵ (D) 9¹²⁵ (E) 4⁵

Solution :

3⁵ + 3⁵+ 3⁵ = 3 (3⁵)

= 3^{(5 + 1)}

= 3⁶

Hence the answer is 3⁶.

Question 5 :

Lindsay has P dollars and mark has $9 less than Lindsay. If mark receives an additional $11, how many dollars will mark now have, in terms of P?

(A) P - 20 (B) 20 - P (C) P + 2 (D) 2 - P (E) P + 11

Solution :

Number of dollars that Lindsay has = P

Number of dollars mark has = P - 9

Number of dollars received by mark additionally = $11

= P - 9 + 11

= P + 2

Hence the number of dollars received by mark is P + 2

Question 6 :

R = 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 11 and S = 3 ⋅ 7 ⋅ 13 ⋅ 17, what is the greatest common factor of R and S ?

(A) 2 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 7 ⋅ 7 ⋅ 11 ⋅ 11 ⋅ 13 ⋅ 17

(B) 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 7 ⋅ 11 ⋅ 13 ⋅ 17

Solution :

Greatest common factor = 3 ⋅ 7

Question 7 :

The counting numbers are placed in order in the chart, as shown. Assuming the pattern continues, in which column will the 200 appear ?

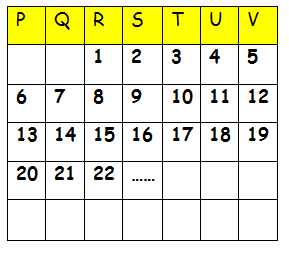
(A) Q (B) S (C) T (D) U (E) V

Solution :

If we write 1 from the first column, we get multiples of 7 in v^th column.

First let us find how many 7's are in 200.

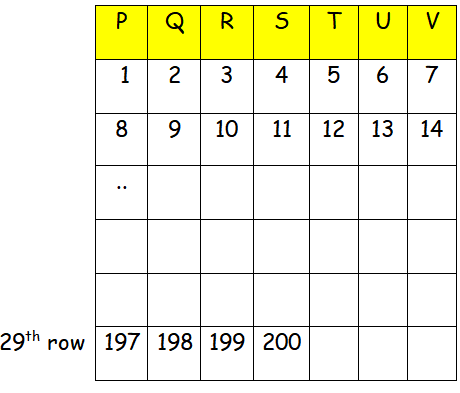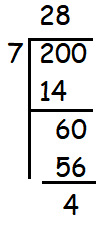7 (28) = 196

From the picture given above, we know that 200 will be in the position of S^th column. Since we started 1 from the column R, we have to move 200 two columns towards the right.

So, 200 will be in U^th column.

Question 8 :

The equation 2(3x + 6) = 3(2x + 4) is satisfied by

(A) No value of x (B) Only negative values of x

(D) only positive values of x (E) all values of x

Solution :

2(3x + 6) = 3(2x + 4)

6x + 12 = 6x + 12

All values of x is the answer.

Question 9 :

Wai ling averaged 84 on her first three exams and 82 on her next 2 exams. What grade must she obtain on her sixth test in order to average 85 for all six exams.

(A) 96 (B) 94 (C) 90 (D) 89 (E) 86

Solution :

By writing the marks scored in six exams

Let "x" be the required mark in sixth subject.

84, 84, 84, 82, 82, x

Average mark = 85

[3(84) + 2(82) + x]/6 = 85

252 + 164 + x = 85(6)

416 + x = 510

x = 510 - 416

x = 94

Hence Wai has to score 94 mark in 6^th exam.