ADDING AND SUBTRACTING DECIMALS
Let us see, how to add the decimals 0.24 and 0.15.
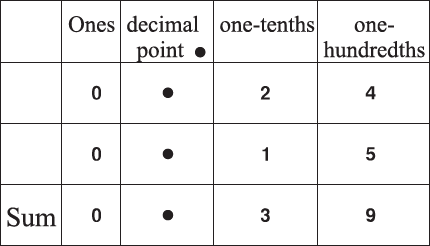
Observe the figure given below.

0.24 and 0.15 are shaded in two different colors. Now the sum of 0.24 and 0.15 is 0.39
That is,
3 tenths and 9 hundredths
Method 1 :
Therefore,
0.24 + 0.15 = 0.39
Method 2 :

Therefore,
0.24 + 0.15 = 0.39
Note :
In both the methods, arrange the decimal numbers according to the place values and add them.
Add : 0.75 and 0.5.
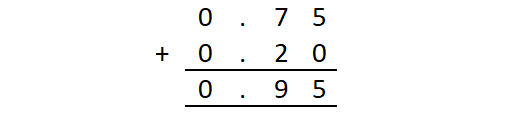
In the above addition of decimals, 0.2 is taken as 0.20, as the first decimal number has two digits on the right side of the decimal point.
Subtracting Decimals
Let us see, how to subtract 0.14 from 0.25.
Method 1 :
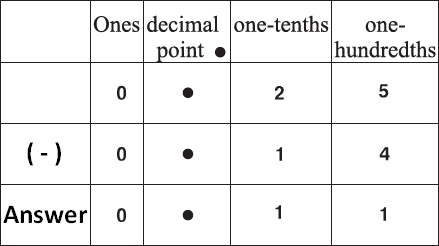
Therefore,
0.25 - 0.14 = 0.11
Method 2 :
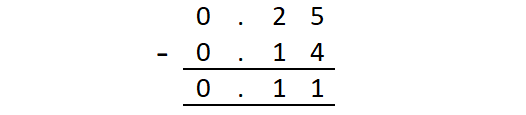
Therefore,
0.25 - 0.14 = 0.11
Note :
In both the methods, arrange the decimal numbers according to the place values and subtract them.
Solved Problems
Problem 1 :
Add the following decimal numbers :
1.23, 0.59, 3.76
Solution :
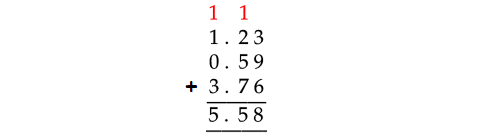
Therefore,
1.23 + 0.59 + 3.76 = 5.58
Problem 2 :
Subtract :
3.79 - 2.56
Solution :
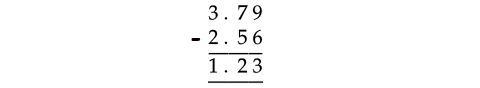
Therefore,
3.79 - 2.56 = 1.23
Problem 3 :
Add the following decimal numbers :
28.07, 7.6, 0.008
Solution :
In the above addition of decimal numbers, 7.6 has to be taken as 7.600 and 28.07 as 28.070. Because the last decimal number has 3 digits to the right of the decimal point.
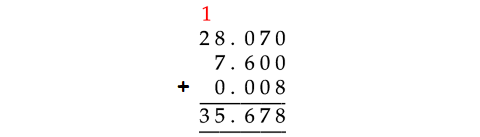
Therefore,
28.07, 7.6, 0.008 = 35.678
Problem 4 :
Add the following decimal numbers :
14.2, 16, 0.542
Solution :
In the above addition of decimal numbers, 14.2 has to be taken as 14.200 and 16 as 16.000. Because the last number has 3 digits to the right of the decimal point.
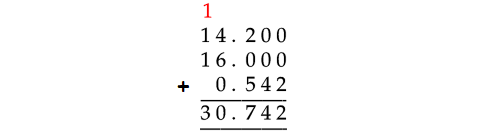
Therefore,
14.2 + 16 + 0.542 = 30.742
Problem 5 :
Add the following decimal numbers :
10.653, 0.065, 3
Solution :
In the above addition of decimal numbers, 3 has to be taken as 3.000. Because, both the first and second numbers have 3 digits to the right of the decimal point.
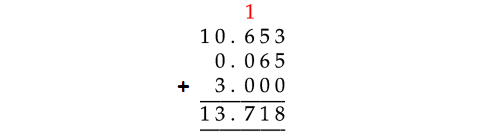
Therefore,
10.653 + 0.065 + 3 = 13.718
Problem 6 :
Add the following decimal numbers :
38.056, 24.6, 32
Solution :
In the given decimal numbers, the first number 38.056 has more number of digits to the right of the decimal point, that is 3.
So, each of the other numbers must have the same number digits to the right of the decimal point, that is 3.
24.6 has to be taken as 24.600 and 39 as 39.000.
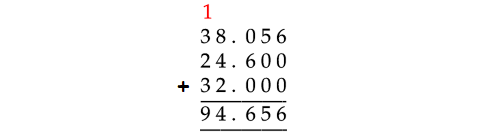
Therefore,
38.056 + 24.6 + 32 = 94.656
Problem 7 :
Find the value of :
29.84 - 13.49
Solution :

Consider the digits at hundredths place.

Since 4 is smaller than 9, we can not subtract 9 from 4.
So, borrow 1 from the preceding number 8 and take that 1 in front of 4. Then, 4 will become 14.
Now, subtract the numbers as shown below.
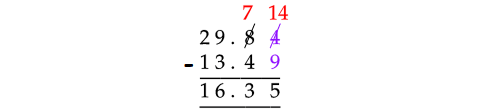
Therefore,
29.84 - 13.49 = 16.35
Problem 8 :
Find the value of :
48.05 - 25.57
Solution :

Consider the digits at hundredths place.

Since 5 is smaller than 7, we can not subtract 7 from 5.
And also, we can not borrow from 1 from the preceding number of 5 in 48.05. Because, it is zero.
So, borrow 1 from 8 at ones place in 48.05 and take that 1 in front of 0. Then, 0 will become 10.
Subtract 1 from 10 and take that 1 in front of 5. Then, it will become 15.
Now, subtract the numbers as shown below.
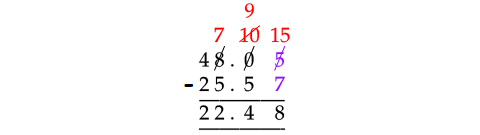
Therefore,
48.05 - 25.57 = 22.48
Problem 9 :
Find the value of :
18 - 6.59
Solution :
In the subtraction of the decimal numbers above, 18 has to be taken as 18.00. Because, the second decimal number has 2 digits to the right of the decimal point.

Consider the digits at hundredths place.

Since 0 is smaller than 9, we can not subtract 9 from 0.
And also, we can not borrow from 1 from the preceding number of 0 in 18.00. Because, it is zero.
So, borrow 1 from 8 at ones place in 18.00 and take that 1 in front of 0. Then, 0 will become 10.
Subtract 1 from 10 and take that 1 in front of 0. Then, it will become 10.
Now, subtract the numbers as shown below.
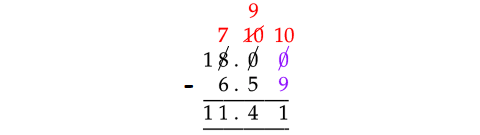
Therefore,
18 - 6.59 = 11.41
Problem 10 :
Find the value of :
8.933 - 3.541
Solution :

Subtract the digits at thousandths place and consider the digits at hundredths place.

Since 3 is smaller than 4, we can not subtract 4 from 3.
So, borrow 1 from 9 at tenths place in 8.933 and take that 1 in front of 3. Then, 3 will become 13.
Now, subtract the numbers as shown below.
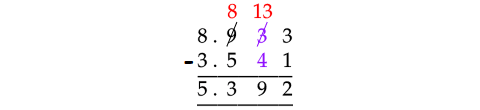
Therefore,
8.933 - 3.541 = 5.392
Practice Questions

Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 113)
Feb 19, 25 04:51 AM
Digital SAT Math Problems and Solutions (Part - 113) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Feb 19, 25 04:48 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 114)
Feb 19, 25 04:45 AM
Digital SAT Math Problems and Solutions (Part - 114)