EXAMPLES OF ADDING AND SUBTRACTING RATIONAL EXPRESSIONS

Example 1 :

Simplify :

(x + 2)/(x + 3)  +  (x - 1)/(x + 3)

Solution :

Because the denominators are same, we have to take the denominator once and combine the numerators. 

=  (x + 2 + x - 1) / (x + 3)

=  (2x + 1) / (x + 3)

Example 2 :

Simplify :

[(x + 1) / (x - 1)²]  +  [1 / (x + 1)]

Solution :

Here, the denominators are not same.

So, we have to find the least common multiple of the denominators.

Least common multiple of the denominators is

(x - 1)²(x + 1)

Then, 

=  [(x + 1)(x + 1)/(x + 1)(x - 1)²]  +  [(x - 1)²/(x + 1)(x -1)²]

=  [(x + 1)²/(x + 1)(x - 1)²]  +  [(x - 1)²/(x + 1)(x -1)²]

=  [(x + 1)²+ (x - 1)²] / (x + 1)(x - 1)²

=  [x² + 2x + 1 + x² - 2x + 1] / (x + 1)(x - 1)²

=  (2x² + 2) / (x + 1)(x - 1)²

Example 3 :

Simplify

[x³/(x - 2)]  +  [8/(2 - x)]

Solution :

Here, the denominators are not same. But, we can do a small adjustment and  make denominator same as shown below.

  =  (x³ + 8)/(x - 2)]  -  8/(x - 2)

Now, the denominators is same. So, we have to take the denominator once and combine the numerators. 

=  [x³/(x - 2)]  -  [8/(x - 2)]

  =  (x³  - 8) / (x - 2)

Use algebraic identity a³ - b³  =  (a - b)(a² + ab + b²) to factor (x³ - 8). 

  =  (x - 2)(x² + 2x + 4) / (x - 2)

  =  x² + 2 x + 4

Example 4 :

Simplify

(x + 2)/(x² + 3x + 2)]  +  (x - 3)/(x² - 2x - 3)

Solution :

x² + 3 x + 2  =  (x + 1)(x +  2)

x² - 2 x - 3  =  (x - 3)(x + 1)

Then, 

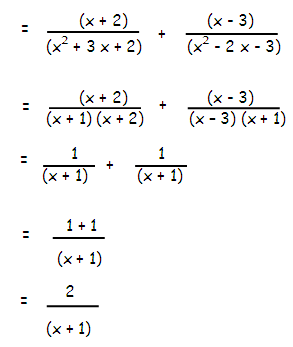
Example 5 :

Simplify

[(x² - x - 6)/(x² - 9)] + [(x² + 2x - 24)/(x² - x - 12)]

Solution :

  =  [(x² - x - 6)/(x² - 9)] + [(x² + 2x - 24)/(x² - x - 12)]

(x² - x - 6)  =  (x - 3)(x + 2)

By comparing (x² - 9) with the algebraic identity 

(a² - b²)  =  (a + b)(a - b)

we get,

(x² - 3²)  =  (x + 3)(x - 3)

(x² + 2 x - 24)  =  (x + 6) (x - 4)

(x² - x - 12)  =  (x - 4) (x + 3)

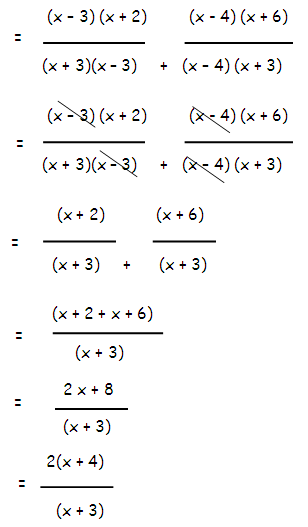
Example 6 :

Simplify

[(2x²-5x+3)/(x²-3x+2)] - [(2x²-7x-4)/(2x² - 3x - 2)]

Solution :

  =  [(2x²-5x+3)/(x²-3x+2)] - [(2x²-7x-4)/(2x² - 3x - 2)]

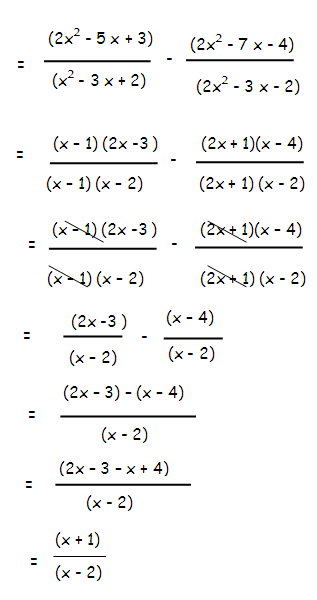
Example 7 :

Simplify

[(x²-4)/(x²+6x+8)]-[(x²-11x+30)/(x²-x - 20)]

Solution :

  =  [(x²-4)/(x²+6x+8)] - [(x²-11x+30)/(x²-x - 20)]

(x² - 2²)  =  (x + 2) (x - 2)

(x²+ 6x + 8)  =  (x + 2) (x + 4)

(x²- 11x + 30)  =  (x - 6) (x - 5)

(x²- x - 20)  =  (x - 5) (x + 4)

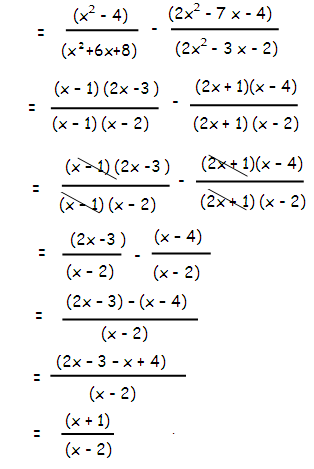
Example 8 :

Simplify

[(2x + 5)/(x + 1)] + [(x² + 1)/(x² - 1)] - [(3x - 2)/(x - 1)]

Solution :

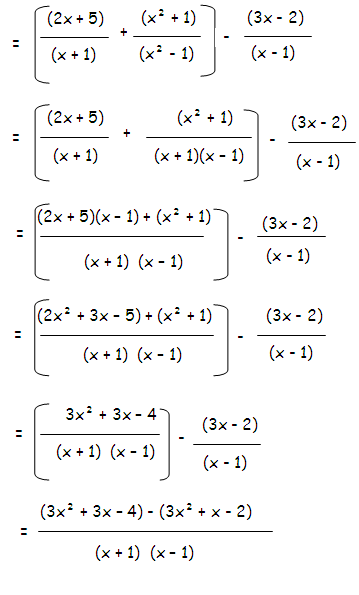
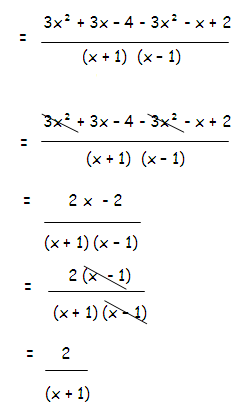
Example 9 :

Simplify

[1/(x²+3x+2)] + [1/(x²+5x+6)] - [2/(x²+4x+3)]

Solution :

(x² + 3x + 2)  =  (x + 1) (x + 2)

(x² + 5x + 6)  =  (x + 2)(x + 3)

(x² + 4x + 3)  =  (x + 3) (x + 1)

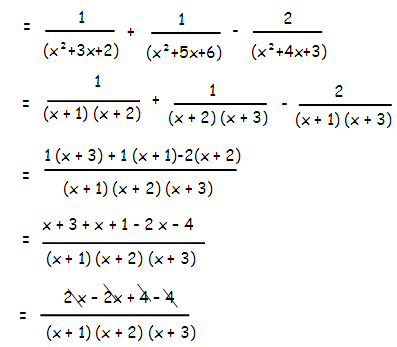
  =  0

Example 10 :

Which rational expression should be added to

(x³ - 1)/(x² + 2) to get (3x³ + 2x² + 4)/(x² + 2) ?

Solution :

let the required rational expression be p(x)

[(x³ - 1)/(x² + 2)]  + p(x)  =  (3x³ + 2x² + 4)/(x² + 2)

p(x)  =  [(3x³ + 2x² + 4)/(x² + 2)] - [(x³ - 1)/(x² + 2)]

Since the denominators are same, we may write only one denominator and combine the numerators.

=  [(3x³ + 2x² + 4) - (x³ - 1)]/(x² + 2)]

=  (3x³ - x³ + 2x² + 4 + 1)/(x² + 2)

=  (2x³ + 2x² + 5)/(x² + 2)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.