ADDITION AND SUBTRACTION OF RATIONAL EXPRESSIONS EXAMPLES
Adding and Subtracting Rational Expressions with Like Denominators :
(i) Add or Subtract the numerators
(ii) Write the sum or difference of the numerators found in step (i) over the common denominator.
(iii) Reduce the resulting rational expression into its lowest form
Adding and Subtracting Rational Expressions with unlike Denominators :
(i) Determine the Least Common Multiple of the denominator.
(ii) Rewrite each fraction as an equivalent fraction with the LCM obtained in step (i). This is done by multiplying both the numerators and denominator of each expression by any factors needed to obtain the LCM.
(iii) Follow the same steps given for doing addition or subtraction of the rational expression with like denominators.
Example 1 :
Which rational expression should be subtracted from
(x2 + 6x + 8)/(x3 + 8) to get 3/(x2 - 2x + 4)
Solution :
Let p(x) be the rational expression should be subtracted.
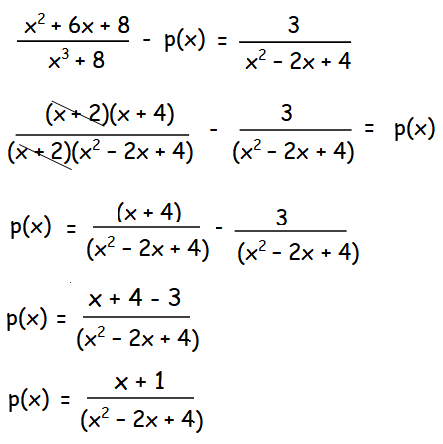
Example 2 :
If A = (2x + 1)/(2x - 1) and B = (2x - 1)/(2x + 1) find 1/(A - B) - 2B/(A2 - B2)
Solution :
= 1/(A - B) - 2B/(A2 - B2)
= [1/(A - B)] - [2B/(A + B)(A - B)]
= (A + B) - 2B/(A + B) (A - B)
= (A + B - 2B) / (A + B) (A - B)
= (A - B) / (A + B) (A - B)
= 1/(A + B)
Now let us apply the values of A and B.
= 1/[(2x + 1)/(2x - 1) + (2x - 1)/(2x + 1)]
= 1/[(2x+ 1)2 + (2x - 1)2/(2x + 1)(2x - 1)]
= (2x + 1)(2x - 1)/[(2x+ 1)2 + (2x - 1)2]
= (4x2 - 1)/[4x2 + 4x + 1 + 4x2 - 4x + 1]
= (4x2 - 1)/(8x2 + 2)
= (4x2 - 1)/2(4x2 + 1)
Example 3 :
If A = x/(x + 1), B = 1/(x + 1), prove that
((A + B)2 + (A- B)2)/(A ÷ B) = 2(x2 + 1)/x(x + 1)2
Solution :
(A + B)2 + (A- B)2 = (A2 + 2AB + B2) + (A2 - 2AB + B2)
= A2 + 2AB + B2 + A2 - 2AB + B2
= 2(A2 + B2)
((A + B)2 + (A- B)2)/(A ÷ B) = 2(A2 + B2)/(A ÷ B)
A2 + B2 = (x/(x + 1))2 + (1/(x + 1))2
= (x/(x + 1)2) + (1/(x + 1)2)
= (x2 + 1)/(x + 1)2
2(A2 + B2) = 2(x2 + 1)/(x + 1)2 ------(1)
(A ÷ B) = [x/(x + 1)] ÷ [1/(x + 1)]
= x/(x + 1) ⋅ (x + 1)/1
= x ------(2)
(1)/(2)
= 2(x2 + 1)/(x + 1)2/x
= 2(x2 + 1)/x(x + 1)2
Hence proved.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
Sum of the Three Angles of a Triangle
Apr 26, 24 09:20 PM
Sum of the Three Angles of a Triangle - Concept - Solved Examples -
Writing Quadratic Functions in Standard Form
Apr 26, 24 12:39 PM
Writing Quadratic Functions in Standard Form or Vertex Form -
Factoring Quadratic Trinomials
Apr 26, 24 01:51 AM
Factoring Quadratic Trinomials - Key Concepts - Solved Problems
