ADJACENT ANGLES WORKSHEET

Question 1 :

What are adjacent angles? Give an example.

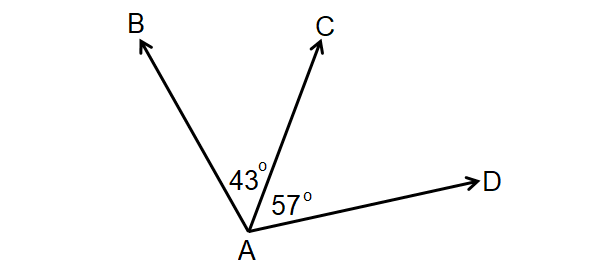
Questions 2-3 : Identify the two pairs of adjacent angles in the given diagram.

Question 2 :

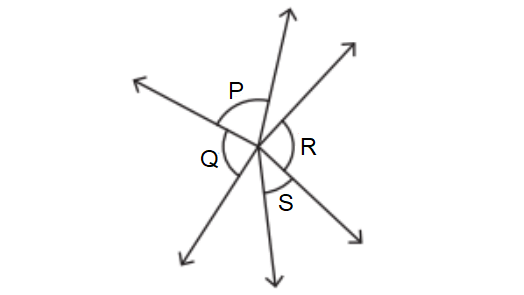
Question 3 :

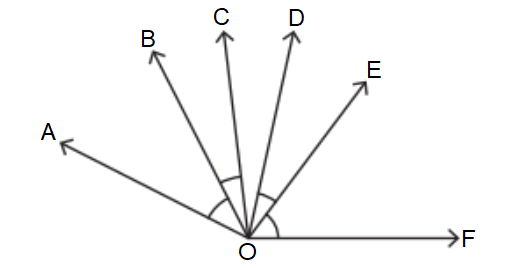
Question 4 :

In the diagram shown below, if ∠XYZ is a right angle, find the value of a.

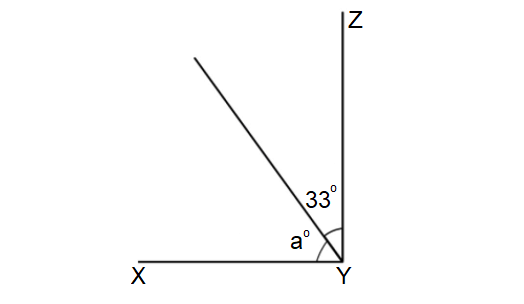
Question 5 :

In the diagram shown below, if ∠ABC is a right angle, find the value of x.

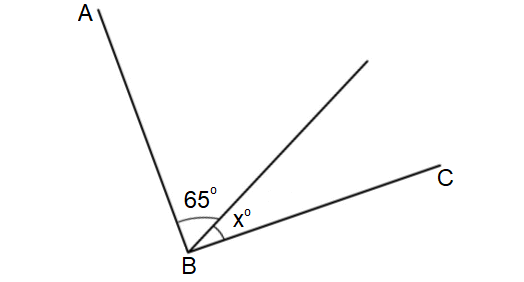
Question 6 :

In the diagram shown below, if ∠EFG is a straight angle, find the value of x.

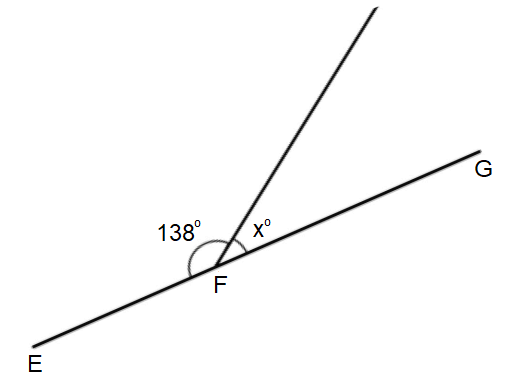
Question 7 :

In the diagram shown below, if ∠WXY is a straight angle, find the value of k.

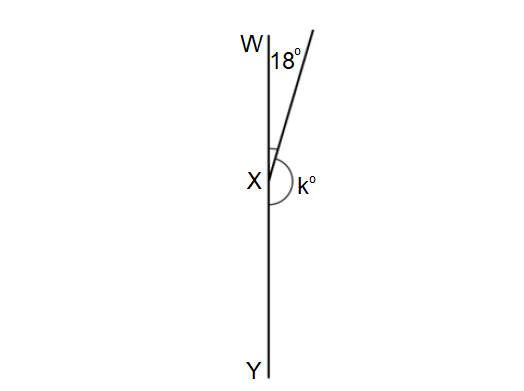
Question 8 :

In the figure given below, if ∠PQR is a straight angle, find the value of y.

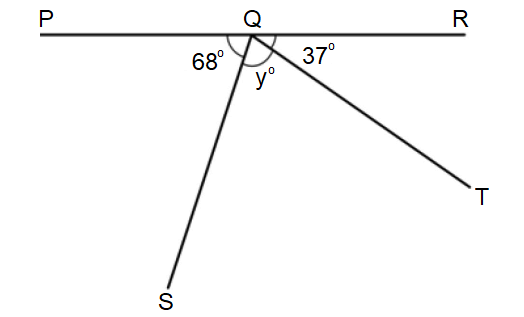
Question 9 :

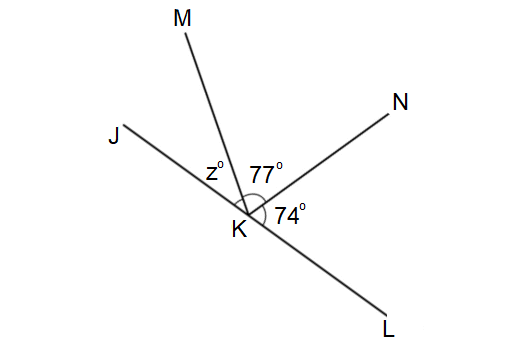
In the figure given below, if ∠JKL is a straight angle, find the value of z.

Question 10 :

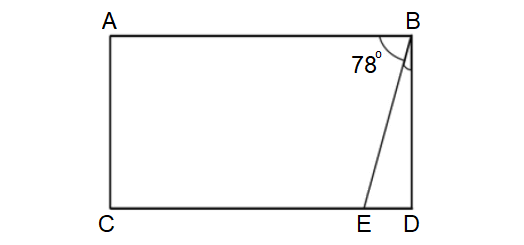
In the diagram shown below, ABCD is a rectangle. Without using a protractor, find m∠EBD.

Question 11 :

The two adjacent angles are complementary. If the first angle is 3° less than twice the second angle, find the two angles.

Question 12 :

The two adjacent angles are supplementary. If the second angle is four times the sum of the first angle and 5°, find the two angles.

Answers

1. Answer :

If two angles have a common vertex and a common side, then they are adjacent angles.

Example :

In the diagram shown above, 43° and 57° are adjacent angles.They have the common vertex A and common side AC.

2. Answer :

∠P and ∠Q

∠R and ∠S

3. Answer :

∠AOB and ∠BOC

∠DOE and ∠EOF

4. Answer :

In the diagram shown above, a° and 33° are adjacent angles and they add up to m∠XYZ.

a° + 33° = m∠ABC

Given : ∠XYZ is a right angle. Then, m∠XYZ = 90°.

a° + 33° = 90°

Subtract 33° from both sides.

(a° + 33°) - 33° = 90° - 33°

a° + 33° - 33° = 57°

a° + 0° = 57°

a° = 57° 

The value of a is 57.

5. Answer :

In the diagram shown above, x° and 65° are adjacent angles and they add up to m∠ABC.

x° + 65° = m∠ABC

Given : ∠ABC is a right angle. Then, m∠ABC = 90°.

x° + 65° = 90°

Subtract 65° from both sides.

(x° + 65°) - 65° = 90° - 65°

x° + 65° - 65° = 25°

x° + 0° = 25°

x° = 25° 

The value of x is 25.

6. Answer :

In the diagram shown above, 138° and x° are adjacent angles and they add up to m∠EFG.

138° + x° = m∠EFG

Given : ∠EFG is a straight angle. Then, m∠EFG = 180°.

138° + x° = 180°

Subtract 145° from both sides.

(138° + x°) - 138° = 180° - 138°

138° + x° - 138° = 42°

x° = 42°

The value of x is 42.

7. Answer :

In the diagram shown above, k° and 18° are adjacent angles and they add up to m∠WXY.

k° + 18° = m∠WXY

Given : ∠WXY is a straight angle. Then, m∠EFG = 180°.

k° + 18° = 180°

Subtract 18° from both sides.

(x° + 18°) - 18° = 180° - 18°

x° + 18° - 18° = 162°

x° + 0° = 162°

The value of x is 162.

8. Answer :

In the figure above, ∠PQS and ∠SQR are adjacent angles and they add up to m∠PQR.

m∠PQS + m∠SQR = m∠PQR

Given : ∠PQR is a straight angle. Then, m∠PQR = 180°.

m∠PQS + m∠SQR = 180°

m∠PQS + m∠SQT + m∠TQR = 180°

Substitute m∠PQS = 68°, m∠SQT = y° and m∠TQR = 37°.

68° + y° + 37° = 180°

y° + 105° = 180°

Subtract 105° from both sides.

(y° + 105°) - 105° = 180° - 105°

y° + 105° - 105° = 75°

y° + 0° = 75°

y° = 75°

The value of y is 75.

9. Answer :

In the figure above, ∠JKM and ∠MKL are adjacent angles and they add up to m∠JKL.

m∠JKM + m∠MKL = m∠JKL

Given : ∠JKL is a straight angle. Then, m∠JKL = 180°.

m∠JKM + m∠MKL = 180°

m∠JKM + m∠MKN + m∠NKL = 180°

Substitute m∠JKM = z°, m∠MKN = 77° and m∠NKL = 74°.

z° + 77° + 74° = 180°

z° + 151° = 180°

Subtract 151° from both sides.

(z° + 151°) - 151° = 180° - 151°

z° + 151° - 151° = 29°

z° + 0° = 29°

z° = 29°

The value of z is 29.

10. Answer :

In the figure above, ∠ABE and ∠EBD are adjacent angles and they add up to m∠ABD.

m∠ABE + m∠EBD = m∠ABD

Since PQST is a rectangle, each interior angle is a right angle. Then, m∠ABD = 90°.

m∠ABE + m∠EBD = 90°

Substitute m∠ABE = 78°.

78° + m∠EBD = 90°

Subtract 78° from both sides.

78° + m∠EBD - 78° = 90° - 78°

m∠EBD = 12°

11. Answer :

Let x° be the second angle.

Then, the first angle is  (2x° - 3°).

Given : The two adjacent angles are complementary.

(2x° - 3°) + x° = 90°

2x - 3 + x = 90

3x - 3 = 90

Add 3 to both sides.  

(3x - 3) + 3 = 90 + 3

3x - 3 + 3 = 93

3x + 0 = 93

3x = 93

Divide both sides by 3.

x = 31

2x - 3 = 2(31) - 3

= 62 - 3

= 59

Therefore, the required angles are 31° and 59°.

12. Answer :

Let x° be the first angle.

Then, the second angle is 4(x° + 5°).

Given : The two adjacent angles are supplementary.

x° + 4(x° + 5°) = 180°

x + 4x + 20 = 180

5x + 20 = 180

Subtract 20 from both sides.

(5x + 20) - 20 = 180 - 20

5x + 20 - 20 = 160

5x + 0 = 160

5x = 160

Divide both sides by 5.

x = 32

4(x + 5) = 4(32 + 5)

= 4(37)

= 148

Therefore, the required angles are 32° and 148°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.