ALGEBRAIC REPRESENTATIONS OF DILATIONS

Example 1 :

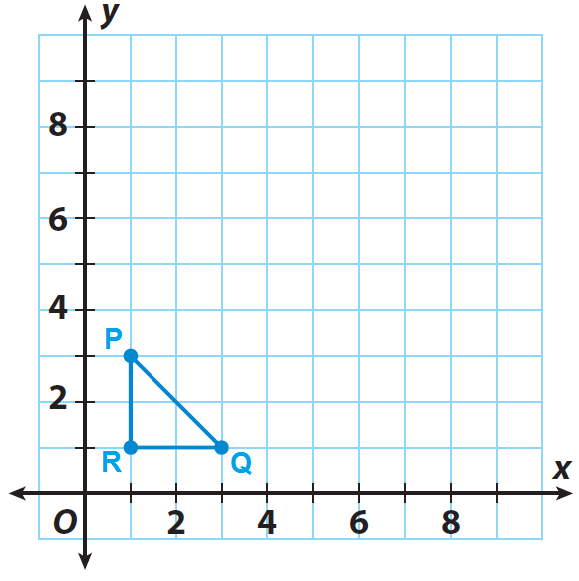
The triangle PQR shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 3, graph the dilated image P'Q'R'.

Solution :

Step 1 :

List the coordinates of the vertices of the pre image.

P(1, 3), Q(3, 1) and R(1, 1)

Step 2 :

Since the scale factor is 3, the rule to get the coordinates of the vertices of the image is

 (x, y) ----> (3x, 3y)

Step 3 :

List the coordinates of the vertices of the image.

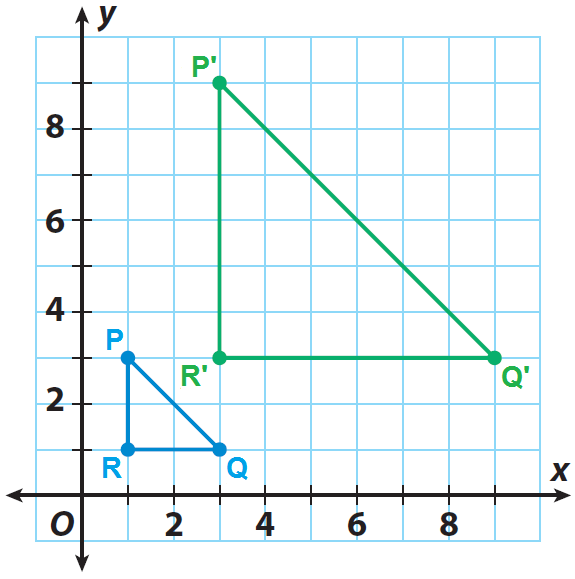
P(1, 3) ----> P'(3, 9)

 Q(3, 1) ----> Q'(9, 3)

R(1, 1) ----> R'(3, 3)

Step 4 :

Graph the image P'Q'R'.

Example 2 :

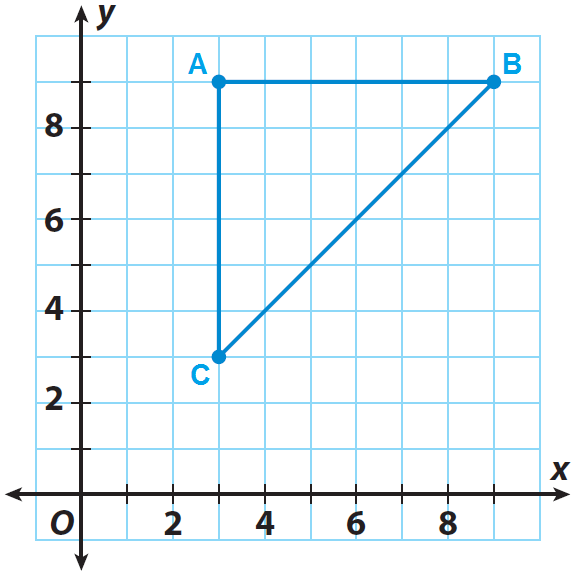
The triangle ABC shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 1/3, graph the dilated image A'B'C'.

Solution :

Step 1 :

List the coordinates of the vertices of the pre image.

A(3, 9), B(9, 9) and C(3, 3)

Step 2 :

Since the scale factor is 1/3, the rule to get the coordinates of the vertices of the image is

 (x, y) → [(1/3)x, (1/3)y]

Step 3 :

List the coordinates of the vertices of the image.

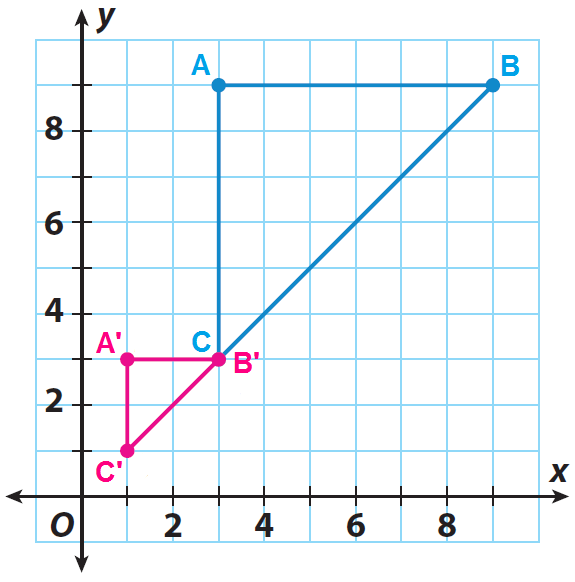
A(3, 9) ----> A'(1, 3)

 B(9, 9) ----> B'(3, 3)

C(3, 3) ----> C'(1, 1)

Step 4 :

Graph the image A'B'C'.

Example 3 :

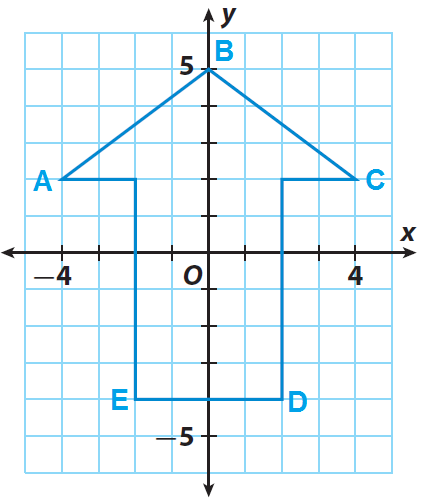
The arrow ABCDE shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 0.5, graph the dilated image A'B'C'D'E'.

Solution :

Step 1 :

List the coordinates of the vertices of the pre image.

A(1, 1), B(3, 1), C(3, 4), D(1, 4) and E(2, 3)

Step 2 :

Since the scale factor is 1/2, the rule to get the coordinates of the vertices of the image is

 (x, y) ----> [0.5x, 0.5y]

Step 3 :

List the coordinates of the vertices of the image.

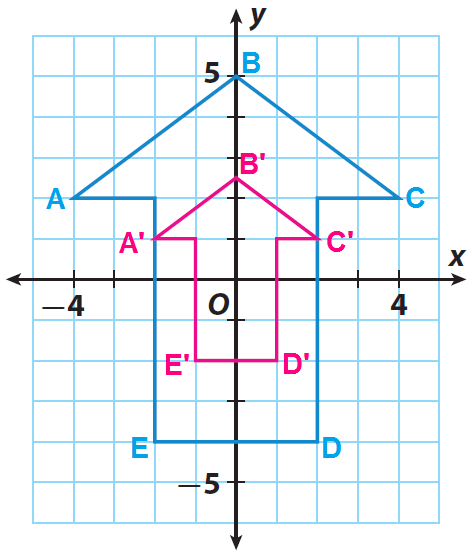
A(-4, 2) ----> A'(-2, 1)

 B(0, 5) ----> B'(0, 2.5)

C(4, 2) ----> C'(2, 1)

D(2, -4) ----> D'(1, -2)

E(-2, -4) ----> E'(-1, -2)

Step 4 :

Graph the image A'B'C'D'E'.

Example 4 :

The rectangle JKLM shown on the grid is the pre-image. If the center of dilation is the origin and the scale factor is 2, graph the dilated image J'K'L'M'.

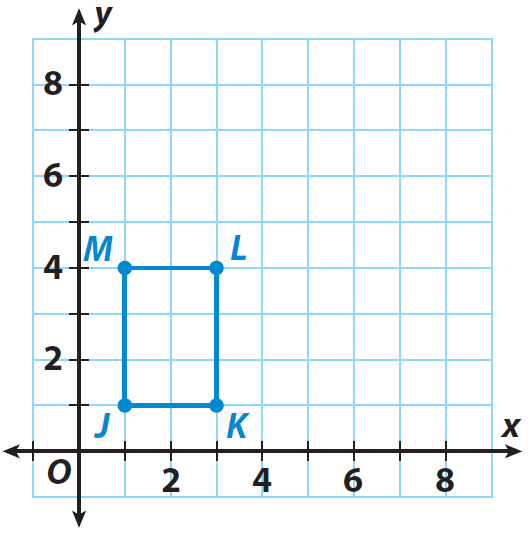
Solution :

Step 1 :

List the coordinates of the vertices of the pre image.

J(1, 1), K(3, 1), L(3, 4) and M(1, 4)

Step 2 :

Since the scale factor is 2, the rule to get the coordinates of the vertices of the image is

 (x, y) ----> (2x, 2y)

Step 3 :

List the coordinates of the vertices of the image.

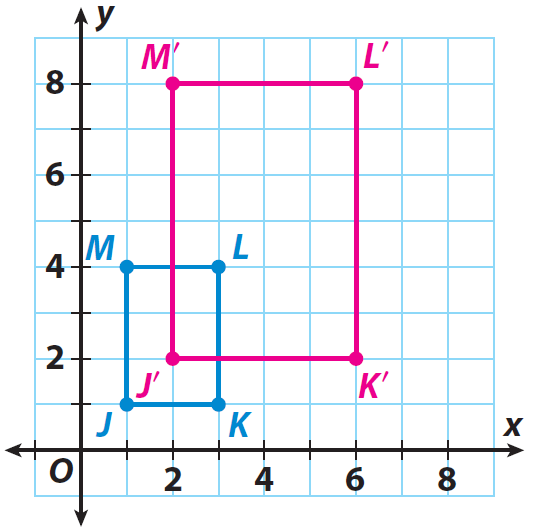
J(1, 1) ----> J'(2, 2)

 K(3, 1) ----> K'(6, 2)

L(3, 4) ----> L'(6, 8)

M(1, 4) ----> M'(2, 8)

Step 4 :

Graph the image J'K'L'M'.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.