ALGEBRAIC REPRESENTATIONS OF TRANSLATIONS

To translate a figure in the coordinate plane, we have to translate each of its vertices. Then, we have to connect the vertices to form the image.

We can use the rules shown in the table which describe how coordinates change when a figure is translated right, left, up, and down on the coordinate plane.

Example 1 :

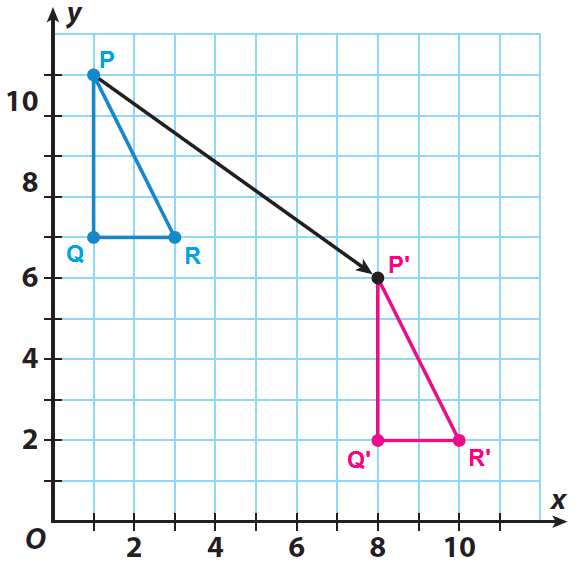
Triangle PQR has the vertices P(1, 11), Q(1, 7) and R(3, 7). Graph the triangle PQR and its image after a translation of 7 units to the right and 5 unit down.

Solution :

Step 1 :

Let P', Q' and R' be the vertices of the translated figure.

Since there is a translation of 7 units to the right and 5 units down, we have to add 7 to x-coordinate and subtract 5 from  y-coordinate of each vertex.

P' ------>  (1+7, 11-5)  =  (8, 6)

Q' ------>  (1+7, 7-5)  =  (8, 2)

R' ------>  (3+7, 7-5)  =  (10, 2)

Step 2 :

Sketch the triangle PQR and its image P'Q'R'.

Example 2 :

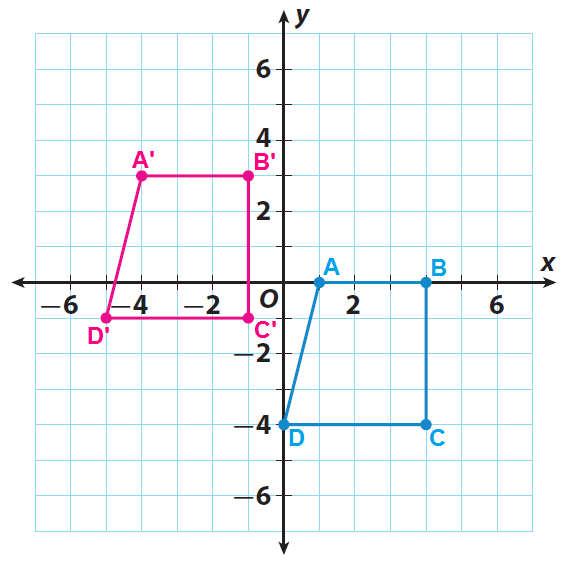
Trapezoid ABCD has the vertices A (1, 0), B(4, 0), C(4, -4) and D(0, -4). Graph the trapezoid ABCD and its image after a translation of 5 units to the left and 3 units up.

Solution :

Step 1 :

Let A', B', C' and D' be the vertices of the translated figure.

Since there is a translation of 5 units to the left and 3 units up, we have to subtract 5 from x-coordinate and add 3 to y-coordinate of each vertex.

A' ------>  (1-5, 0+3)  =  (-4, 3)

B' ------>  (4-5, 0+3)  =  (-1, 3)

C' ------>  (4-5, -4+3)  =  (-1, -1)

D' ------>  (0-5, -4+3)  =  (-5, -1)

Step 2 :

Sketch the trapezoid ABCD and its image A'B'C'D'.

Example 3 :

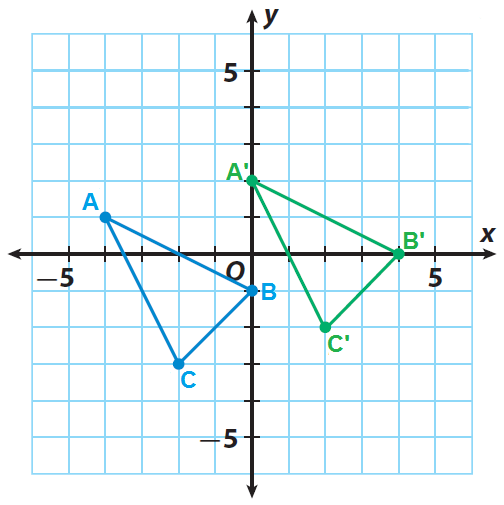
Triangle ABC has the vertices A (-4, 1), B(0, -1) and C(-2, -3). Graph the triangle ABC and its image after a translation of 4 units to the right and 1 unit up.

Solution :

Step 1 :

Let A', B' and C' be the vertices of the translated figure.

Since there is a translation of 4 units to the right and 1 unit up, we have to add 4 to x-coordinate and add 1 to y-coordinate of each vertex.

A' ------>  (-4+4, 1+1)  =  (0, 2)

B' ------>  (0+4, -1+1)  =  (4, 0)

C' ------>  (-2+4, -3+1)  =  (2, -2)

Step 2 :

Sketch the triangle ABC and its image A'B'C'.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.