ALLIGATION OR MIXTURE

Key Concept

1. Alligation or Mixture :

This is a rule which we can use to find the ratio in which we have to mix two or more types of ingredients to produce the mixture in a desired price.

2. Mean price :

The cost price of the mixture per given unit is called mean price.

3. Rule to find the ratio for producing mixtures :

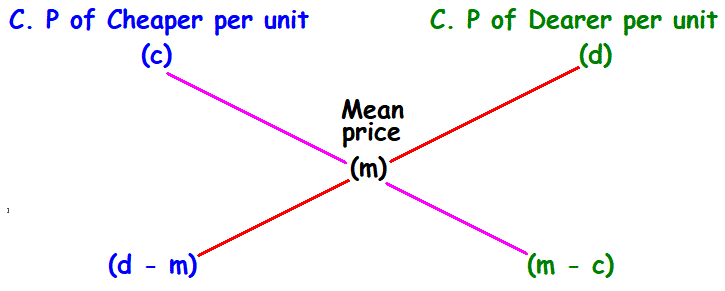
To produce the mixture, the ratio in which the cheaper and dearer to be mixed is

= (d - m) : (m - c)

4. Say, a bucket has x units of liquid. From which y units of liquid taken out and replaced by water. After repeating this process n times, the quantity of pure liquid is

Example 1 :

What is the ratio in which the two types of wheat mixed where the price of the first type is $9.30 per kg and the second type is $10.80 per kg so the mixture is having worth $10 per kg?

Solution :

From the given information, we have

cost price of the cheaper (c) = $9.30

cost price of the dearer (d) = $10.80

cost price of the mixture (m) = $10

 Rule to find the ratio for producing mixture is

= (d - m) : (m - c)

So, we have

(d - m) : (m - c) = (10.8 - 10) : (10 - 9.3)

(d - m) : (m - c) = 0.8 : 0.7

(d - m) : (m - c) = 8 : 7

So, the ratio in which the first kind and second kind to be mixed is 8 : 7.

Problem 2 :

Find the ratio in which, water to be mixed with milk to gain 20% by selling the mixture at cost price.

Solution :

Let us consider the water as cheaper and milk as dearer.

Let the cost price of 1 ltr of pure milk be $1 and water be $0.

Now we take some quantity of milk (less than 1 ltr), add some water and make it to be 1 ltr milk-water mixture.

Let x be the cost price in 1 ltr of the mixture.

Because the gain is 20%, selling price of 1 ltr of the mixture is

= x + 20% of x

= x +  ²⁰ˣ⁄₁₀₀

= ¹⁰⁰ˣ⁄₁₀₀ +  ²⁰ˣ⁄₁₀₀

= ⁽¹⁰⁰ˣ ⁺ ²⁰ˣ⁾⁄₁₀₀

= ¹²⁰ˣ⁄₁₀₀

= ⁶ˣ⁄₅

Given : The mixture is sold at the cost price of pure milk.

That is,

S.P of 1 ltr of mixture = C.P of 1 ltr of pure milk

⁶ˣ⁄₅ = 1

Multiply  both sides by ⅚.

x = ⅚

So, the cost price of 1 ltr of the mixture is $⅚.

Now, we can consider the following points.

Cheaper : Cost price of 1 ltr water (c) = $0

Dearer : Cost price of 1 ltr pure milk (d) = $1

Mean price : Cost price of 1 ltr mixture (m) = $⅚.

Rule to find the ratio for producing mixture is

= (d - m) : (m - c)

Then, we have

(d - m) : (m - c) = (1 - ⅚) : (⅚ - 0)

(d - m) : (m - c) = ⅙ : ⅚

(d - m) : (m - c) = 1 : 5

So, water and milk  have to be mixed in the ratio to gain 20% is 1 : 5.

Problem 3 :

The milk and water in two vessels A and B are in the ratio 4:3 and 2:3 respectively. In what ratio, the liquids in vessels A and B be mixed to obtain a new mixture in vessel C consisting half milk and half water?

Solution :

Let the cost price of 1 liter pure milk be $1.

Amount of milk in 1 liter of mixture in A = ⁴⁄₇ liters

Amount of milk in 1 liter of mixture in B = ⅖ liters

Amount of milk in 1 liter of mixture in C = ½ liters

Let us assume the cost price of the liquid mixture in A as cheaper, B as dearer and C as mean price.

cost price of 1 liter mixture in A (c) = $⁴⁄₇

cost price of 1 liter mixture in B (d) = $⅖

cost price of 1 liter mixture in C (m) = $½

Rule to find the ratio for producing mixture is

= (d - m) : (m - c)

So, we have

(d - m) : (m - c) = (⅖ - ½) : (½ - ⁴⁄₇)

(d - m) : (m - c) =  ⁽⁴ ⁻ ⁵⁾⁄₁₀ : ⁽⁷ ⁻ ⁸⁾⁄₁₄

(d - m) : (m - c) = -⅒ : -¹⁄₁₄

(d - m) : (m - c) = ⅒ : ¹⁄₁₄

Least common multiple of (10, 14) is 70.

So, multiply both the terms of the ratio ⅒ : ¹⁄₁₄ by 70.

(d - m) : (m - c) = ⁷⁰⁄₁₀ : ⁷⁰⁄₁₄

(d - m) : (m - c) = 7 : 5

So, the ratio in which the liquids in vessels A and B be mixed is 7 : 5.

Problem 4 :

A dealer mixes tea costing $6.92 per kg with tea costing $7.77 per kg and sells the mixture at $8.80 per kg and earns a profit of 17.5 % on his sale price. In what ratio does he mix them?

Solution :

Given : The mixture is sold at $8.80 per kg and 17.5% profit earned on the sale price.

Profit = 17.5% of 8.80

Profit = 0.175 ⋅ 8.80

Profit = 1.54

Then the cost price of of the mixture is

= Selling price - Profit

= 8.80 - 1.54

= 7.26

Let the cost price of tea costing $6.92 per kg as cheaper and $7.77 as dearer.

Then the mean price is $7.26.

More clearly,

cheaper (c) = 6.92

dearer (d) = 7.77

mean price (m) = 7.26

Rule to find the ratio for producing mixture is

= (d - m) : (m - c)

So, we have

(d - m) : (m - c) = (7.77 - 7.26) : (7.26 - 6.92)

(d - m) : (m - c) = 0.51 : 0.34

(d - m) : (m - c) = 51 : 34

(d - m) : (m - c) = 3 : 2

So, the required ratio is 3 : 2.

Problem 5 :

A container has 10 liters of milk. 1 liter of liquid is taken out and replaced by water. If this processed is repeated thrice, find the amount of pure milk in the container.

Solution :

The formula to find the amount of pure milk is,

= x ⋅ (1 - ʸ⁄ₓ)ⁿ

Here,

x = 10 ltrs

y = 1 ltr

n = 3

Then, we have

= 10 ⋅ (1 - ⅒)³

= 10 ⋅ (¹⁰⁄₁₀ - ⅒)³

= 10 ⋅ (⁹⁄₁₀)³

= 10 ⋅ (0.9)³

= 10 ⋅ 0.729

= 7.29

So, the amount of pure milk in the container will be 7.29 liters.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.