ALTERNATE EXTERIOR ANGLES THEOREM

Alternate Exterior Angles :

When two parallel lines are cut by a transversal, the pair of angles formed outside the parallel lines but on the opposite sides of the transversal are called alternate exterior angles. 

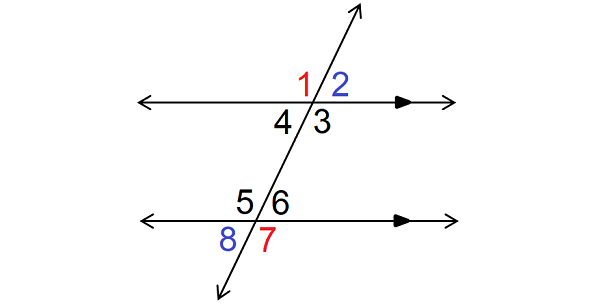
In the figure above, ∠1 and ∠7 are alternative exterior angles, and also ∠2 and ∠8 are alternate exterior angles. 

Alternate Exterior Angles Theorem :

If two parallel lines are cut by a transversal, then Alternate Exterior Angles are congruent. 

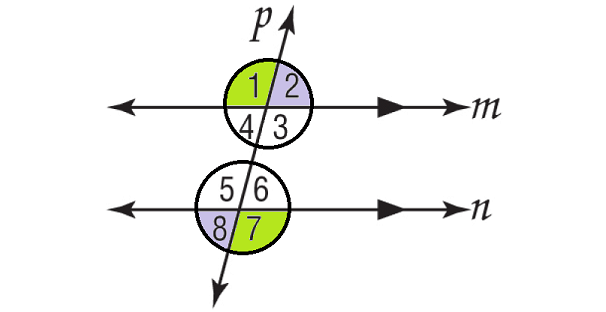
Given : m||n, p is transversal. 

Prove : ∠1 and ∠7 are congruent and ∠2 and ∠8 are congruent. 

Proof :

Since m || n, by the Corresponding Angles Postulate, 

∠1 ≅ ∠5

By the Vertical Angles Theorem, 

m∠5 ≅ m∠7

B y the Transitive Property of Congruence, 

∠1 ≅ ∠7

We can prove that m∠2 ≅ m∠8 using the same method. 

Alternate Exterior Angles Theorem – Converse

When two parallel lines are cut by a transversal, if alternate exterior angles have equal measure, then the two lines are parallel. 

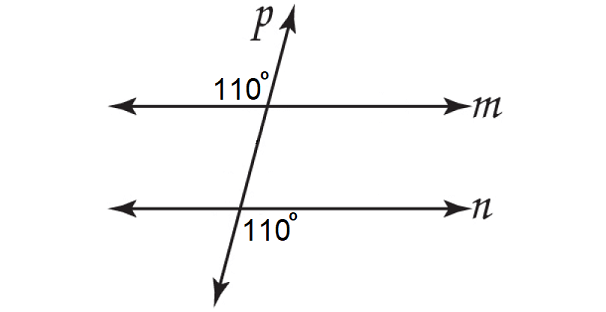
In the figure above, lines m and n are parallel. Because, a pair of alternate exterior angles have equal measure. 

Example 1 :

In the figure shown below, m∠8 = 75°. Find m∠1.

Solution :

In the figure above, lines m and n are parallel, ∠7 and ∠8 form a linear pair. 

m∠7 + m∠8  =  180°

Substitute m∠8 = 75°. 

m∠7 + 75°  =  180°

Subtract 75° from each side. 

m∠7  =  105°

∠1 and ∠7 are alternate exterior angles.

∠1 ≅ ∠7

m∠1  =  m∠7

Substitute m∠7 = 105°.

m∠1  =  105°

Example 2 :

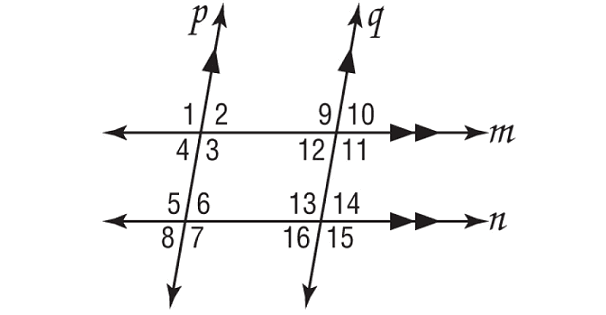
In the figure shown below, m∠2 = 78°. Find the measures of ∠8, ∠10 and ∠16.

Solution :

In the figure above, lines m and n are parallel, p and q are parallel.

∠2 and ∠8 are alternate exterior angles. 

∠2 ≅ ∠8

m∠2  =  m∠8

Substitute m∠2 = 78°.

78°  =  m∠8

∠8 and ∠16 are corresponding angles. 

∠8 ≅ ∠16

m∠8  =  m∠16

Substitute m∠8 = 78°. 

78°  =  m∠16

∠10 and ∠16 are alternate interior angles. 

∠10 ≅ ∠16

m∠10  =  m∠16

Substitute m∠16 = 102°. 

m∠10  =  102°

Therefore, 

m∠8  =  102°

m∠10  =  102°

m∠16  =  102°

Example 3 :

In the figure shown below, lines m and n are parallel and p is transversal. Find the value of x. 

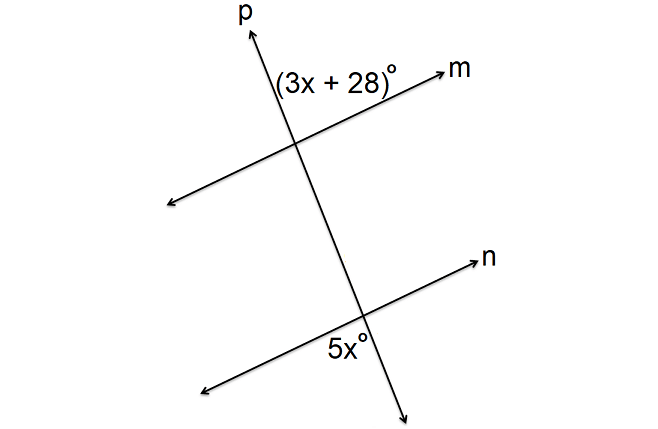
Solution :

In the figure above m and n are parallel and p is transversal. Angles 5x° and (3x + 28)° are alternate exterior angles and they are congruent. 

By the definition of congruent angles, 

5x°  =  (3x + 28)°

5x  =  3x + 28

Subtract 3x from each side. 

2x  =  28

Divide each side by 2.

x  =  14

Example 4 :

In the figure shown below, solve for x. 

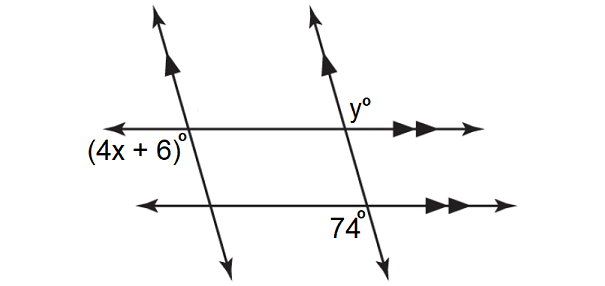
Solution :

In the figure above, y° and 74° are alternate exterior angles and they are equal.

y°  =  74°

(4x + 6)° and y° are alternate exterior angles and they are equal.

(4x + 6)°  =  y°

Substitute y° = 74°.

(4x + 6)°  =  74°

4x + 6  =  74

Subtract 6 from each side. 

4x  =  68

Divide each side by 4.

x  =  17

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.