ANGLE ANGLE SIMILARITY WORKSHEET

In each case, explain whether two triangles are similar using Angle-Angle Similarity Theorem.

Problem 1 :

Problem 2 :

Problem 3 :

Answers

1. Answer :

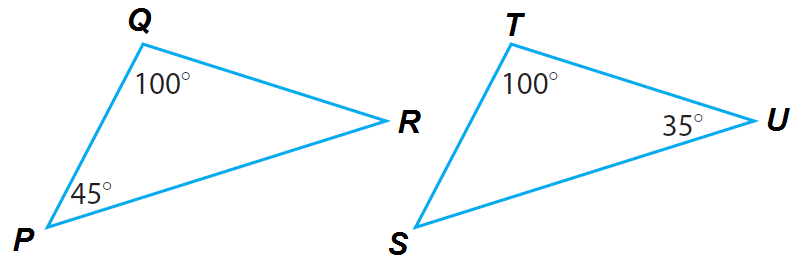
The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.

Triangle PQR : 

Write the Triangle Sum Theorem for this triangle.

m∠P + m∠Q + m∠R  =  180°

Substitute the given angle measures.

45° + 100° + m∠R  =  180°

Simplify.

145° + m∠R  =  180°

Subtract 145° from both sides.

145° + m∠R - 145°  =  180° - 145°

Simplify.

m∠R  =  35°

Triangle STU : 

Write the Triangle Sum Theorem for this triangle.

m∠S + m∠T + m∠U  =  180°

Substitute the given angle measures.

m∠S + 100° + 35°  =  180°

Simplify.

m∠S + 135°  =  180°

Subtract 135° from both sides.

m∠S + 135° - 135°  =  180° - 135°

Simplify.

m∠S  =  45°

Conclusion :

Three Angles of triangle PQR are 45°, 100° and 35°.

Three Angles of triangle STU are 45°, 100° and 35°.

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

2. Answer :

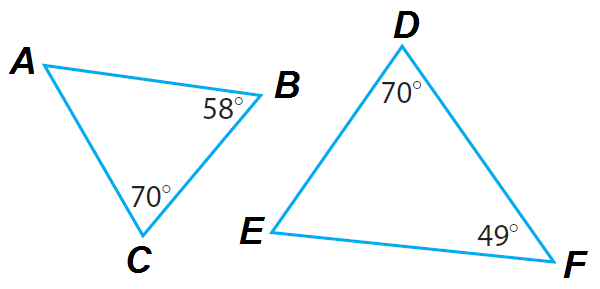
The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.

Triangle ABC : 

Write the Triangle Sum Theorem for this triangle.

m∠A + m∠B + m∠C  =  180°

Substitute the given angle measures.

m∠A + 58° + 70°  =  180°

Simplify.

m∠A + 128°  =  180°

Subtract 128° from both sides.

m∠A + 128° - 128°  =  180° - 128°

Simplify.

m∠A  =  52°

Triangle DEF : 

Write the Triangle Sum Theorem for this triangle.

m∠D + m∠E + m∠F  =  180°

Substitute the given angle measures.

70° + m∠E + 49°  =  180°

Simplify.

m∠E + 119°  =  180°

Subtract 119° from both sides.

m∠E + 119° - 119°  =  180° - 119°

Simplify.

m∠E  =  61°

Conclusion :

Three Angles of triangle ABC are 52°, 58° and 70°.

Three Angles of triangle DEF are 70°, 61° and 49°.

Because only one angle is congruent, the two triangles are not similar.

3. Answer :

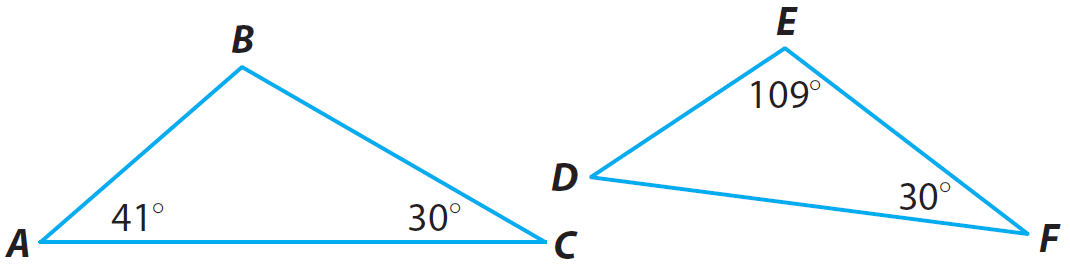
The figure shows only one pair of congruent angles. Find the measure of the third angle in each triangle.

Triangle ABC : 

Write the Triangle Sum Theorem for this triangle.

m∠A + m∠B + m∠C  =  180°

Substitute the given angle measures.

41° + m∠B + 30°  =  180°

Simplify.

m∠B + 71°  =  180°

Subtract 71° from both sides.

m∠B + 71° - 71°  =  180° - 71°

Simplify.

m∠B  =  109°

Triangle DEF : 

Write the Triangle Sum Theorem for this triangle.

m∠D + m∠E + m∠F  =  180°

Substitute the given angle measures.

m∠D + 109° + 30°  =  180°

Simplify.

m∠D + 139°  =  180°

Subtract 130° from both sides.

m∠D + 139° - 139°  =  180° - 139°

Simplify.

m∠D  =  41°

Conclusion :

Three Angles of triangle ABC are 41°, 109° and 30°.

Three Angles of triangle DEF are 41°, 109° and 30°.

Because two angles in one triangle are congruent to two angles in the other triangle, the two triangles are similar.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.