ANGLE BETWEEN TWO CURVES

Angle between two curves, if they intersect, is defined as the acute angle between the tangent lines to those two curves at the point of intersection.

For the given curves, at the point of intersection using the slopes of the tangents, we can measure

the acute angle between the two curves. Suppose

y = m₁x + c₁ and y = m₂x + c₂

are two lines, then the acute angle θ between these lines is given by,

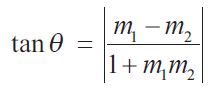
(i) If the two curves are parallel at (x₁, y₁), then

m₁  =  m₂

(ii) If the two curves are perpendicular at (x₁, y₁) and if m₁ and m₂ exists and finite then

m₁ x m₂  =  -1

Problem 1 :

Find the angle between the rectangular hyperbola xy = 2 and the parabola x² + 4y = 0 .

Solution :

Slope of rectangular hyperbola :

x(dy/dx) + y(1)  =  0

dy/dx  =  -y/x

Slope of parabola :

x² + 4y = 0 

2x+4(dy/dx)  =  0

dy/dx  =  -2x/4

dy/dx  =  -x/2

To find point of intersection of the curves.

y  =  x/2  ----(1) and y  =  -x²/4 ----(2)

-x²/4  =  x/2

-x³  =  8

x³  =  -8

x³  =  (-2)³

x  =  -2

By applying x  =  -2 in (1), we get

y  =  -2/2

y  =  -1

At (-2, -1)

Angle between the above curves  :

m₁ - m₂  =  -1/2 - 1  =  -3/2

m₁ x m₂  =  -1/2 x 1  =  -1/2

tan θ  =  |(-3/2)/1-(-1/2)|

tan θ  =  |(-3/2)/(1/2)|

 θ  =  tan^-1(3)

Problem 2 :

Show that the two curves x² − y² = r² and xy = c² where c, r are constants, cut orthogonally

Solution :

If two two curves are intersecting orthogonally, then 

m₁ x m₂  =  -1

x² − y² = r² 

2x-2y(dy/dx)  =  0

-2y(dy/dx)  =  -2x

m₁  =  dy/dx  =  -x/y  -----(1)

 xy = c²

x(dy/dx) + y(1)  =  0

m₂  =  dy/dx  =  -y/x  -----(2)

m₁ x m₂  =  (-x/y) (-y/x)

=  -1

So, the given curves are intersecting orthogonally.

Problem 3 :

If the curves y = 2e^x & y = ae^-x intersect orthogonally, What is the value of a ?

Solution :

If two two curves are intersecting orthogonally, then 

m₁ x m₂  =  -1

y = 2e^x

m₁ = dy/dx = 2e^x -----(1)

y = ae^-x

dy/dx = ae^-x (-1)

m₂  = - ae^-x -----(2)

m₁ x m₂  = (2e^x) (- ae^-x)

-1 =  -2ae^x-x

-1 =  -2ae⁰

1 = 2a(1)

2a = 1 

a = 1/2

When the given curves are intersecting orthogonally, the value of a is 1/2.

Problem 4 :

Show that the curves x = y² & xy = k cut at right angles if 8k²= 1 

Solution :

x = y² ------(1)

xy =k ------(2)

Finding slope from (1), 

1 = 2y(dy/dx)

m₁ = dy/dx = 1/2y

Finding slope from (2), 

x(dy/dx) + y(1) = 0

m₂ = dy/dx = -y/x

Finding the point of intersection of the curves :

Applying (1) in (2), we get

y² y = k

y³ = k

y = k^1/3

Applying the value of y in x = y², we get

x = (k²)^1/3

x = k^2/3

When the tangent lines drawn for the curve meet at right angle, we understand that the curves are perpendicular.

(1/2y) x (-y/x) = -1

-1/2x = -1

2k^2/3  = 1

(2k^2/3)³ = 1³

8k² = 1

Hence it is proved.

Problem 5 :

At what point on the curve y = x² does the normal make an angle of 30 clockwise with the x-axis

Solution :

y = x²

dy/dx = 2x

Slope of tangent = 2x

Slope of normal = -1/2x ----(1)

m = tan θ

m = tan 30

m = 1/√3 ----(2)

(1) = (2)

-1/2x = 1/√3

√3 = -2x

x = -√3/2

Applying the value of x, we get

y = (-√3/2)²

y = 3/4

So, the required point is (-√3/2, 3/4)

Problem 6 :

Find the co-ordinates of the point on the curve

x^1/2 + y^1/2 = 4

at which tangent is equally inclined to the axes.

Solution :

Since the tangent line that we draw makes equal angle with x-axis and y-axis.

So, the required angle is 45 degree.

m = tan θ

m = tan 45

m = 1

x^1/2 + y^1/2 = 4

√x + √y = 4 -----(1)

Differentiating with respect to x, we get

1/2√x + (1/2√y)dy/dx = 0

(1/2√y)dy/dx = - 1/2√x

dy/dx = -2√y/2√x

dy/dx = -√y/√x

Slope = 1

-√y/√x = 1

√x = -√y

Squaring both sides, we get

x = y

Applying the value of x in √x + √y = 4

√x + √x = 4

2√x = 4

√x = 4/2

√x = 2

Squaring both sides

x = 4

y = 4

So, the required point is (4, 4).

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.