ANGLE BISECTOR THEOREM PROOF

Theorem

The internal (external) bisector of an angle of a triangle divides the opposite side internally (externally) in the ratio of the corresponding sides containing the angle.

Case (i) (Internally) :

Given : In ΔABC, AD is the internal bisector of ∠BAC which meets BC at D.

To prove : BD/DC = AB/AC.

Construction : Draw CE ∥ DA to meet BA produced at E.

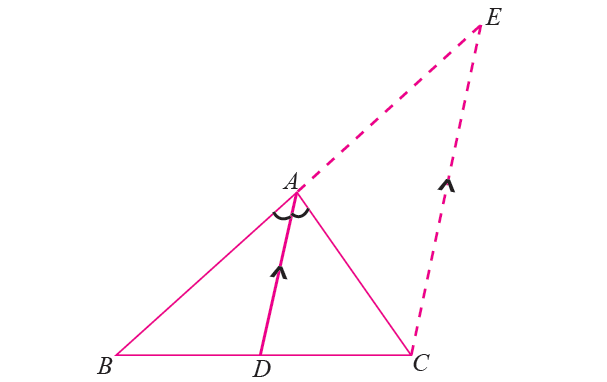
Proof (Internally) : 

Because CE ∥ DA and AC is the transversal, we have

∠DAC = ∠ACE (alternate angles) -----(1)

and

∠BAD = ∠AEC (corresponding angles) -----(2)

Because AD is the angle bisector of ∠A,

∠BAD = ∠DAC -----(3)

From (1), (2) and (3), we have

∠ACE = ∠AEC

Thus in ΔACE, we have

AE = AC

(Sides opposite to equal angles are equal)

Now, in ΔBCE we have, CE ∥ DA.

By Thales Theorem,

BD/DC = BA/AE

Because AE = AC,

BD/DC = AB/AC

Hence the theorem.

Case (i) (Externally) :

Given : In ΔABC, AD is the external bisector of ∠BAC and intersects BC produced at D.

To prove : BD/DC = AB/AC

Construction : Draw CE ∥ DA meeting AB at E.

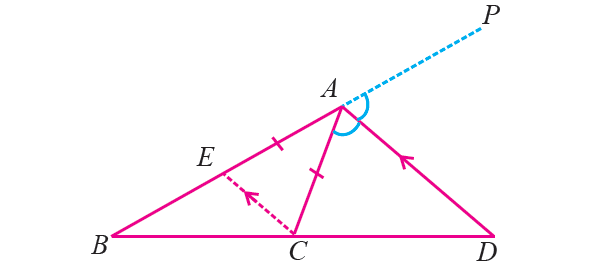
Proof (Externally) :

Because CE ∥ DA and AC is a transversal, we have

∠ECA = ∠CAD (alternate angles) ----(1)

Also, CE ∥ DA and BP is a transversal, we have

∠CEA = ∠DAP (corresponding angles) ----(2)

But AD is the bisector of ∠CAP,

∠CAD = ∠DAP ----(3)

From (1), (2) and (3), we have

∠CEA = ∠ECA

(Sides opposite to equal angles are equal)

In ΔBDA, we have EC ∥ AD.

By Thales Theorem,

BD/DC = BA/AE

Because AE = AC,

BD/DC = BA/AC

Hence the theorem.

Solved Problems

Problem 1 :

In the ΔABC shown below, find the length of BD.

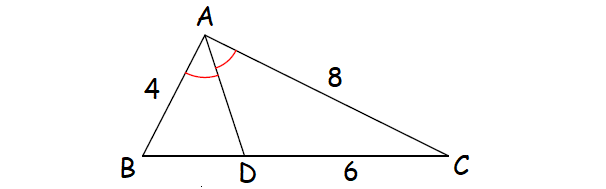
Solution :

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

BD/DC = AB/AC

Substitute.

BD/6 = 4/8

BD/6 = 1/2

Multiply each side by 6.

BD = 3

Problem 2 :

In the ΔABC shown below, find the length of CD.

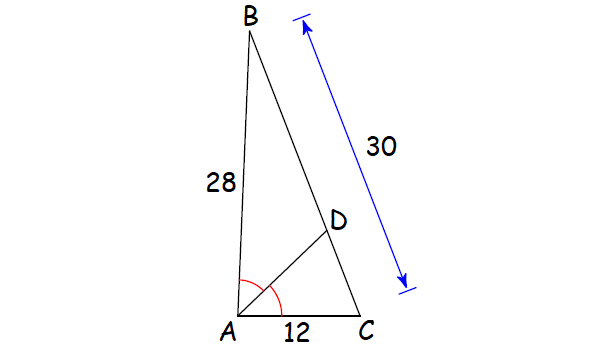
Solution :

Let x be the length of CD.

Then the length of DB = 30 - x.

Since AD is the angle bisector of ∠A, by Angle Bisector Theorem,

CD/DB = AC/AB

Substitute.

x/(30 - x) = 12/28

x/(30 - x) = 3/7

7x = 3(30 - x)

7x = 90 - 3x

Add 3x to each side.

10x = 90

Divide each side by 10.

x = 9

CD = 9

Problem 3 :

Solve for x.

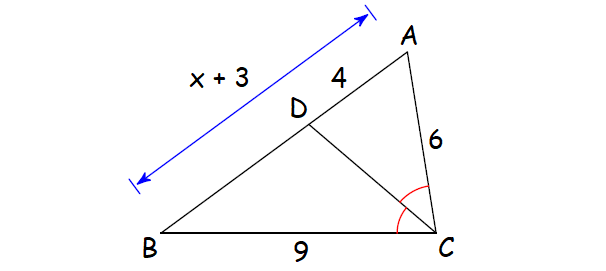
Solution :

Find the length of DB :

DB = AB - AD

= (x + 3) - 4

= x + 3 - 4

= x - 1

Since CD is the angle bisector of ∠C, by Angle Bisector Theorem,

AD/DB = CA/CB

Substitute.

4/(x - 1) = 6/9

4/(x - 1) = 2/3

3(4) = 2(x - 1)

12 = 2x - 2

Add 2 to each side.

14 = 2x

Divide each side by 2.

7 = x

Problem 4 :

Solve for x.

Solution :

Find the length of AD :

AD = AC - DC

= 18 - 8

= 10

Since BD is the angle bisector of ∠B, by Angle Bisector Theorem,

CD/DA = BC/BA

Substitute.

8/10 = (2x - 4)/15

4/5 = (2x - 4)/15

15(4) = 5(2x - 4)

60 = 10x - 20

Add 20 to each side of the equation.

80 = 10x

Divide each side by 10.

8 = x

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.