ANGLE MEASURES IN TRIANGLES WORKSHEET

1. The measure of one acute angle of a right triangle is two times the measure of the other acute angle. Find the measure of each acute angle. 

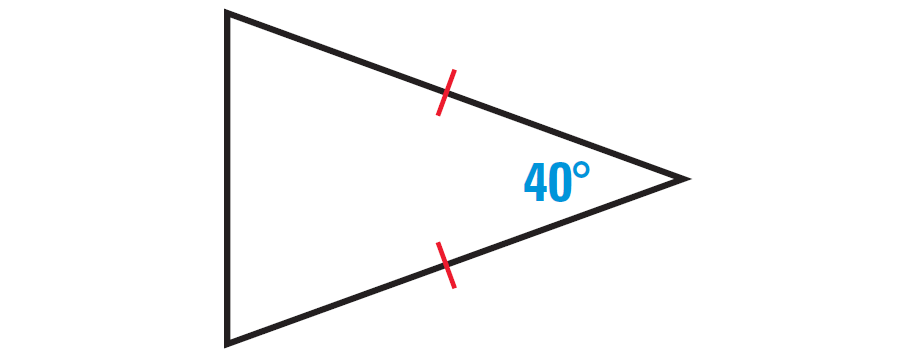
2. Find the missing angles in the triangle shown below. 

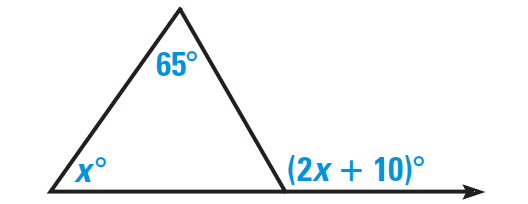
3. Find the value of x in the diagram shown below. 

4. Find the missing angles in the triangle shown below. 

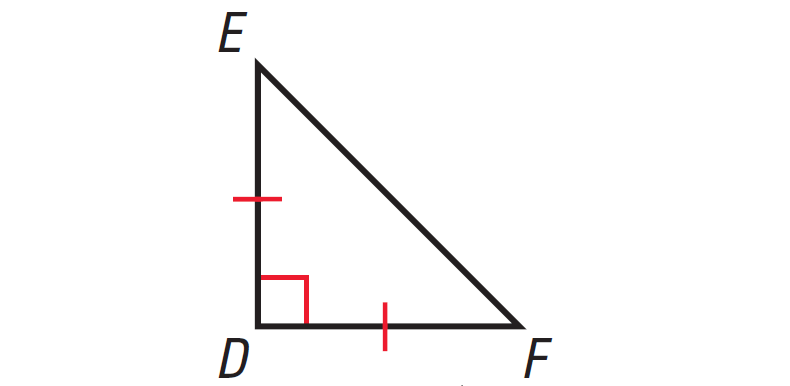
1. Answer :

Let A, B and C be the vertices of the triangle and right angle is at C. 

Let ∠A = x°, then ∠B = 2x°. The diagram shown below illustrates this. 

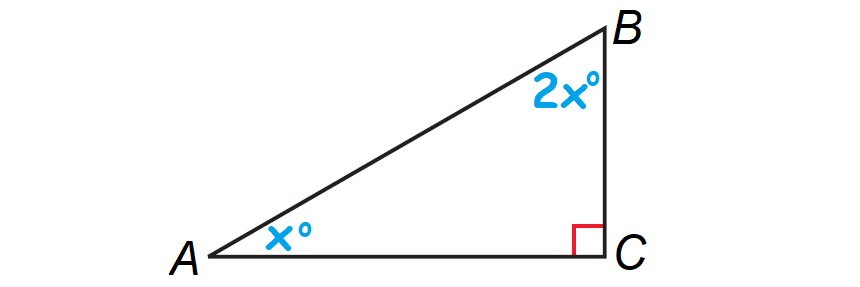
By Corollary to the Triangle Sum Theorem, the acute angles of a right triangle are complementary.  

x° + 2x° = 90°

3x° = 90°

Divide both sides by 3.

x = 30

So, m∠A = 30° and m∠B = 2(30°) = 60°.

Hence, the two acute angles are 30° and 60°. 

2. Answer :

In the triangle shown above, two sides are congruent. Angles opposite to congruent sides are always congruent. 

So, if one missing angle is assumed to be x°, then the other missing angle also must be x°. Because the two angles are congruent. 

The diagram shown below illustrates this. 

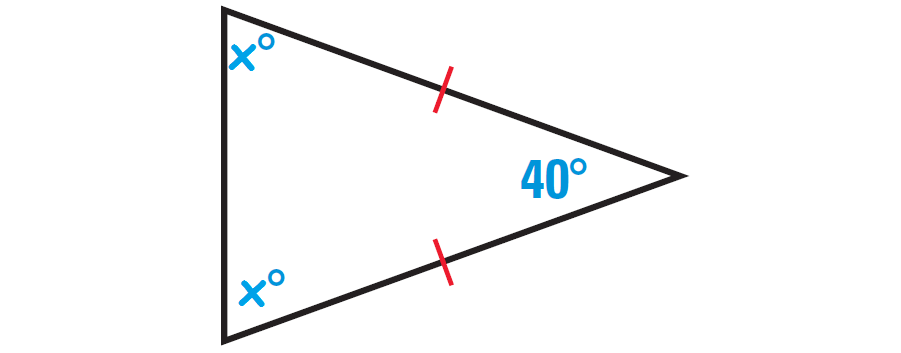
By Triangle Sum Theorem, the sum of the measures of the interior angles of a triangle is 180°. 

x° + x° + 40° = 180°

2x + 40 = 180

Subtract 40 from both sides. 

2x = 140

Divide both sides by 2. 

x = 70 

Hence, the measure of each missing angle is 70°.

3. Answer :

By Exterior Angle Theorem, the measure of an exterior angle of a triangle is equal to the sum of the measures of the two nonadjacent interior angles. 

x° + 65° = (2x + 10)°

x + 65 = 2x + 10

Subtract x from both sides. 

65 = x + 10

Subtract 10 from both sides. 

55 = x

4. Answer :

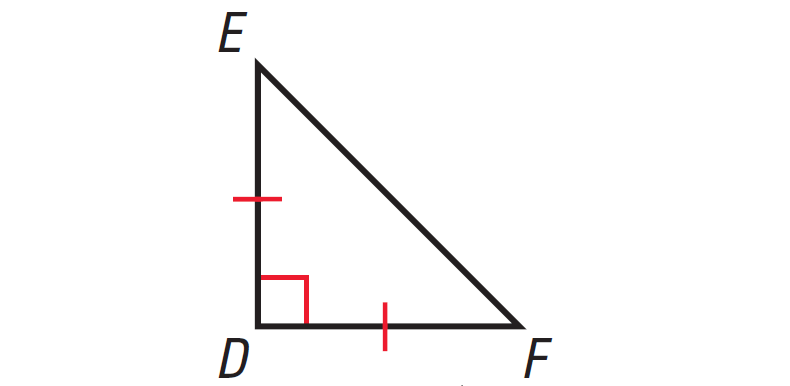
In the triangle shown above, two sides are congruent. Angles opposite to congruent sides are always congruent. 

So, if one missing angle is assumed to be x°, then the other missing angle also must be x°. Because the two angles are congruent. 

The diagram shown below illustrates this. 

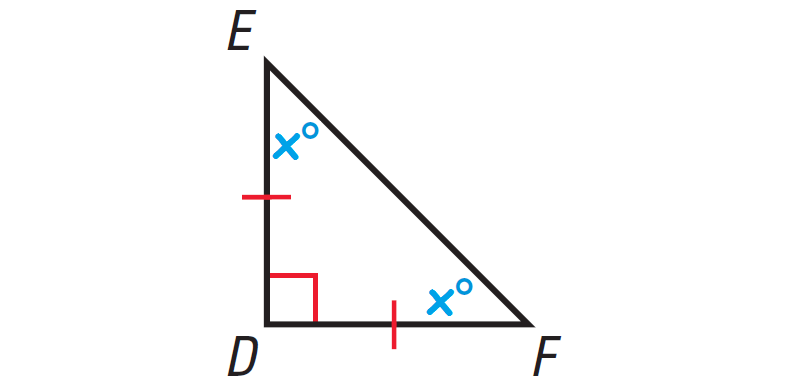
In the triangle shown above, one of the angles is right angle. So, it is right triangle.

By Corollary to the Triangle Sum Theorem, the acute angles of a right triangle are complementary.  

x° + x° = 90°

2x = 90

Divide both sides by 2. 

x = 45

Hence, the measure of each missing angle is 45°.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.