ANGLE OF ELEVATION AND DEPRESSION EXAMPLES

Example 1 :

A student sitting in a classroom sees a picture on the black board at a height of 1.5 m from the horizontal level of sight. The angle of elevation of the picture is 30°. As the picture is not clear to him, he moves straight towards the black board and sees the picture at an angle of elevation of 45°. Find the distance moved by the student.

Solution :

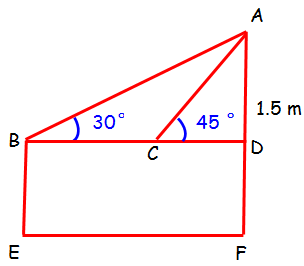
Distance moved by the student  =  BC

In triangle ABD :

∠ABD  =  30°

  tan θ = opposite side/Adjacent side

tan 30°  =  AD/BD

1/√3  =  1.5/BD

BD  =  1.5 x √3 ==> 1.5 √3

In triangle ACD :

∠ACD  =  45°

  tan θ = opposite side/Adjacent side

tan 45°  =  AD/CD

1  =  1.5/CD

CD  =  1.5

BC  =  BD - CD  

BC  =  1.5 √3 - 1.5

=  1.5 (√3 - 1) = 1.5(1.732 - 1)

=  1.5 (0.732) ==> 1.098 m

Hence the distance moved by the student is 1.098 m.

Example 2 :

A boy is standing at some distance from a 30 m tall building and his eye level from the ground is 1.5 m. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

Solution :

From the given information, we can draw a rough diagram 

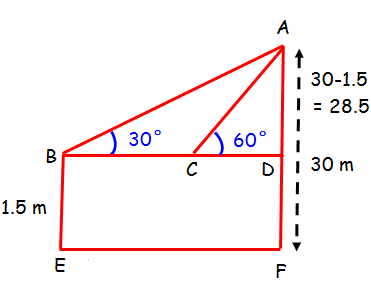
AD  =  28.5 m 

In triangle ABD

∠ABD  =  30°

  tan θ = opposite side/Adjacent side

  tan 30° = AD/BD

  1/√3  =  28.5/BD ==> BD  = 28.5 √3 --(1)

In triangle ACD

∠ABD  =  60°

  tan θ = opposite side/Adjacent side

  tan 60° = AD/CD

  √3  =  28.5/CD ==> CD  = 28.5/√3 

Multiplying by √3 on both numerator and denominator, we get

CD  =  28.5/√3 ==> 28.5√3/3  ==> 9.5√3  -->(2)

the distance he walked towards the building =  BD - CD 

  =  28.5 √3  -  9.5√3 ==> 19√3 m

Example 3 :

From the top of a lighthouse of height 200 feet, the lighthouse keeper observes a Yacht and a Barge along the same line of sight .The angles of depression for the Yacht and the Barge are 45° and 30°  respectively. For safety purposes the two sea vessels should be at least 300 feet apart. If they are less than 300 feet , the keeper has to sound the alarm. Does the keeper have to sound the alarm ?

Solution : 

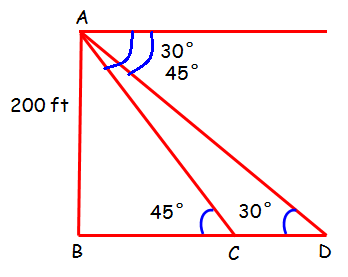
From the above picture, we have to find the value of CD.

In triangle ABC

∠ACB  =  45°

sin θ = opposite side/Hypotenuse side

sin 45°  =  AB/BC

1/√2  =  200/BC

BC  =  200 √2

In triangle ABD

∠ADB  =  30°

sin 30°  =  AB /BD

1/2  =  200/BD

BD = 200 x 2 ==> 400

CD = BD - BC ==> 400 - 200 √2 ==> 200(2 - √2)

  =  200 (2 - 1.414)

  =  200(0.586) ==> 117.2 m

From this, we come to know that the distance between  Yacht and a Barge is less than 300 m. Hence the keeper has to sound the alarm.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.