ANGLE OF ELEVATION AND DEPRESSION WORKSHEET

1. The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30° . If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiations control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms.

2. The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find (i) The height of the lamp post. (ii) The difference between height of the lamp post and the apartment. (iii) The distance between the lamp post and the apartment. (√3 = 1.732)

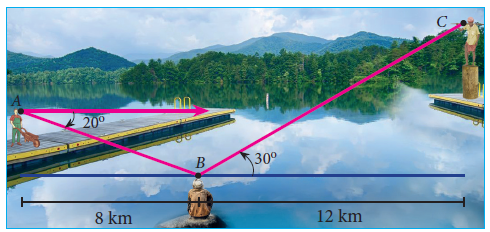
3. Three villagers A, B and C can see each other across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30° . Calculate : (i) the vertical height between A and B. (ii) the vertical height between B and C. (tan 20° = 0.3640, √3 = 1.732)]

1. Answer :

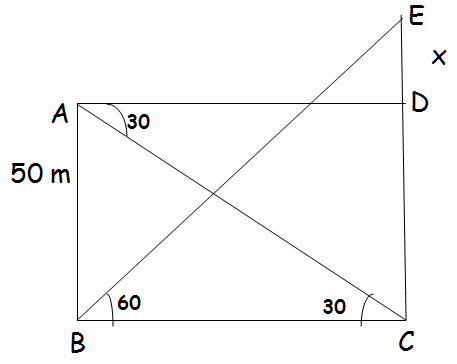
In triangle BEC,

tanθ = Opposite side/Adjacent side 

tan60° = EC/BC

√3 = (50 + x)/BC

BC = (50 + x)/√3 ----(1)

In triangle ABD,

tan30° = AB/BC

1/√3 = 50/BC

BC = 50√3 ----(2)

(1) = (2)

(50 + x)/√3 = 50√3

50 + x = 50√3√3

50 + x = 150

x = 150 - 50

x = 100

Height of cell phone tower = 100 + 50

  = 150 m

Hence the cell phone tower meets the radiation norms.

2. Answer :

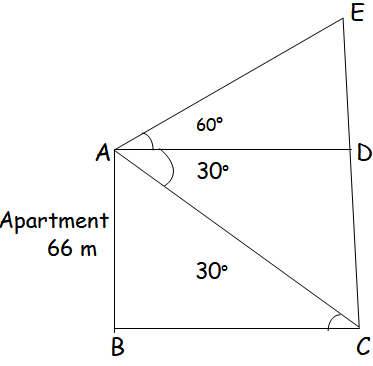
In triangle AED,

tan 60 = ED/AD

√3 = ED/AD

AD = ED/√3 ----(1)  

In triangle ABC,

tan 30 = AB/BC

1/√3 = 66/BC

BC = 66√3 ----(2)  

(1) = (2)

ED/√3 = 66√3

ED = 66(3)

ED = 198

(i)  Height of lamp post = ED + DC

= 198 + 66

= 264 m

(ii) The difference between height of the lamp post and the apartment

= 264 - 66

= 198 m

(iii) The distance between the lamp post and the apartment

BC = 66√3

= 66(1.732)

= 114.31 m

3. Answer : 

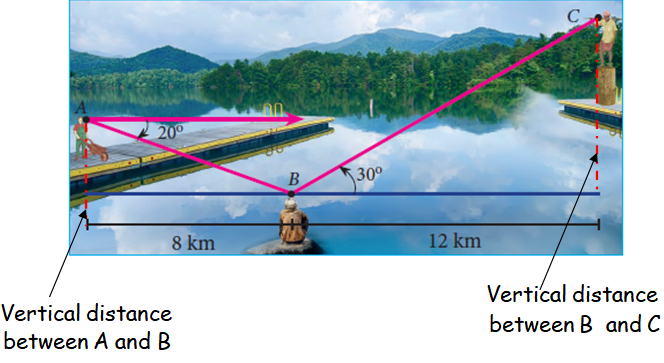
In the left side triangle,

tan 20 = Vertical distance of AB/8

 0.3640 = Vertical distance of AB/8

Vertical distance of AB = 0.3640(8)

Vertical distance of AB = 2.91 km

In the right side triangle,

tan 30 = Vertical distance of BC/12

1/√3 = Vertical distance of BC/12

Vertical distance of BC = 12/√3

= 12(√3/3)

= 4√3

= 4(1.732)

= 6.928

Vertical distance of BC = 6.93 km.

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.