ANGLE OF ELEVATION PRACTICE PROBLEMS

Problem 1 :

Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height 10√3 m.

Solution :

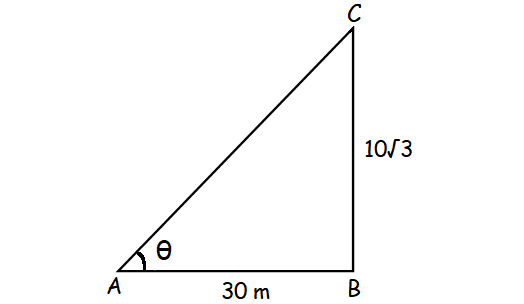
BC - height of the tower

∠B = 90°

AC = hypotenuse side, BC = opposite side, AB = Adjacent side

Here we have to find θ,  known sides are opposite and adjacent. Based on this information, we have to use tan θ.

tan θ  =  Opposite side / Adjacent side

tan θ  =  BC/AB

  tan θ  =  10√3/30

  tan θ  = √3/3

  tan θ  = 1/√3

θ  =  tan^-1(1/√3)

 θ  =  tan^-1(1/√3)

θ  =  30° or π/6

Problem 2 :

A road is flanked on either side by continuous rows of houses of height 4√3 m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30° . Find the width of the road.

Solution :

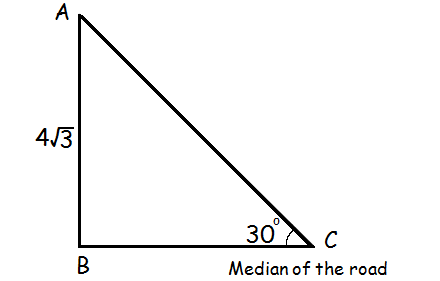
AB = opposite side, BC = Adjacent side, AC = hypotenuse side

tan θ  =  Opposite side / Adjacent side

tan 30  =  AB/BC

1/√3  =  4√3/Distance from median of the road to house

BC  =  4√3(√3)  =  12

Width of the road :

=  2(BC)

=  2(12)

=  24 m

Problem 3 :

A tower stands vertically on the ground. From a point on the ground, which is 48 m away from the foot of the  tower, the angle of elevation of the top of the tower is 30° . Find the height of the tower.

Solution :

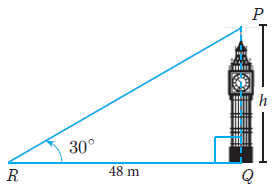
In the triangle PRQ,

Opposite side = h, hypotenuse = PR and adjacent side = PQ

tan θ = Opposite side / adjacent side

tan 30 = PQ / RQ

1/√3 = h/48

h = 48 / √3

Rationalizing the denominator, we get

h = 48√3/3

h = 16√3

Then, height of the tower is 16√3 m.

Problem 4 :

A kite is flying at a height of 75 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60° . Find the length of the string, assuming that there is no slack in the string.

Solution :

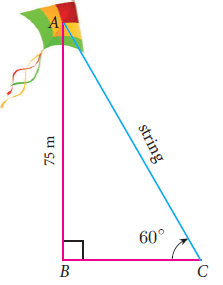
Length of string = hypotenuse

In triangle ABC, AB = opposite side

BC = Adjacent side

AC = Hypotenuse

sin θ = Opposite side / Hypotenuse

sin 60 = AB / AC

√3/2 = 75/AC

AC = 75(2) / √3

Rationalizing the denominator, we get

AC = 150 / √3

= 150√3/3

= 50√3

So, the length of the string is 50√3 m.

Problem 5 :

Two ships are sailing in the sea on either sides of a lighthouse. The angle of elevation of the top of the lighthouse as observed from the ships are 30° and 45° respectively. If the lighthouse is 200 m high, find the distance between the two ships. (√3 = 1.732 )

Solution :

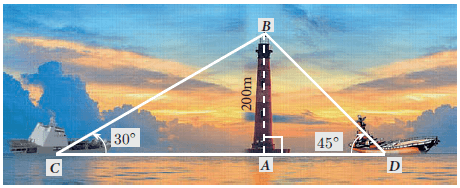
In triangles ABC and ABD.

tan θ = Opposite side / adjacent side

tan 30 = AB / AC

1/√3 = 200/AC

AC = 200√3 --(1)

tan 45 = AB / AD

1 = 200/AD

AD = 200 --(2)

Distance between two ships = AC + AD

= 200√3 + 200

= 200(√3 + 1)

= 200(1.732 + 1)

= 200(2.732)

= 546.4 m

So, the distance between two ships is 546.4 m.

Problem 6 :

From a point on the ground, the angles of elevation of the bottom and top of a tower fixed at the top of a 30 m high building are 45° and 60° respectively. Find the height of the tower. (√3 = 1.732)

Solution :

In triangle ABP,

tan θ = Opposite side / adjacent side

tan 45 = AB / BP

1 = 300 / BP

BP = 300 ----(1)

tan 60 = (AB + AC) / BP

√3 = (300 + h) / BP

BP = (300 + h)/√3 ----(2)

(1) = (2)

300 = (300 + h) / √3

300 √3 = 300 + h

h = 300√3 - 300

h = 300(√3 - 1)

= 300(1.732 - 1)

= 300 (0.732)

h = 219.6

Height of the tower = 300 + 219.6

= 519.6 m

So, the height of the tower is 519.6 m.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.