ANGLE PAIRS AND ONE STEP EQUATIONS

Vertical angles are the opposite angles formed by two intersecting lines. Vertical angles are congruent because the angles have the same measure.

Adjacent angles are pairs of angles that share a vertex and one side but do not overlap.

Complementary angles are two angles whose measures have a sum of 90°.

Supplementary angles are two angles whose measures have a sum of 180°. We discovered in the Explore Activity that adjacent angles formed by two intersecting lines are supplementary.

Example 1 :

Look at the diagram given below and answer the question.  

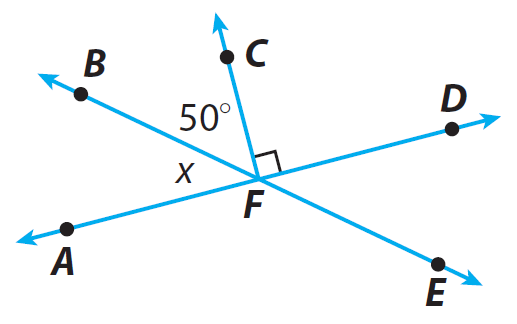
A. Name a pair of vertical angles :

Vertical angles are opposite angles formed by intersecting lines.

∠AFB and ∠DFE are vertical angles.

B. Name a pair of adjacent angles :

Adjacent angles share a vertex and a side but do not overlap.

∠AFB and ∠BFD are adjacent angles.

C. Name a pair of supplementary angles :

Adjacent angles formed by intersecting lines are supplementary.

∠AFB and ∠BFD are supplementary angles.

D. Name two pairs of supplementary angles that include <DFE :

Any angle that forms a line with ∠DFE is a supplementary angle to ∠DFE.

∠DFE and ∠EFA are supplementary angles, as are ∠DFE and ∠DFB.

E. Find the measure of angle <AFB :

Use the fact that ∠AFB and ∠BFD in the diagram are supplementary angles to find m∠AFB.

∠AFB + ∠BFD  =  180°

From the given diagram, we have ∠AFD  =  x and also

m∠BFD  =  50° + 90°  =  140°

x + 140°  =  180°

Subtract 140° from both sides. 

(x + 140°) - 140°  =  180° - 140°

x  =  40°

The measure of m∠AFB is 40°.

Example 2 :

Find the value of 'x' in the diagram given below. 

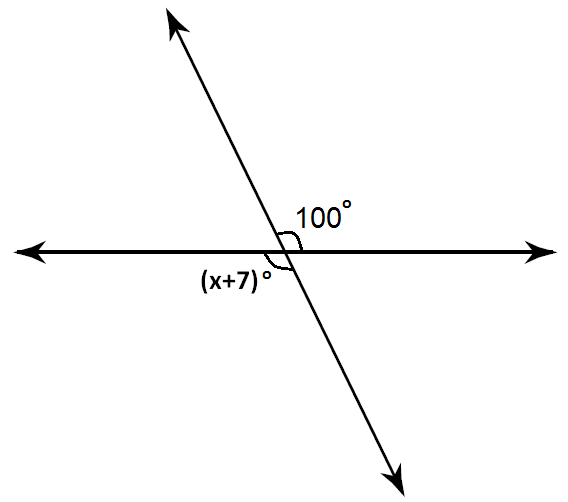
Solution :

From the picture above, it is very clear (x+7)° and 100° are vertical angles and also they are congruent.  

So, we have

x + 7  =  100

Subtract 7 from both sides

(x + 7) - 7  =  100 - 7

x  =  93

So, the value of 'x' is 93. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.