ANGLE PAIRS AND TWO STEP EQUATIONS WORKSHEET

Problem 1 :

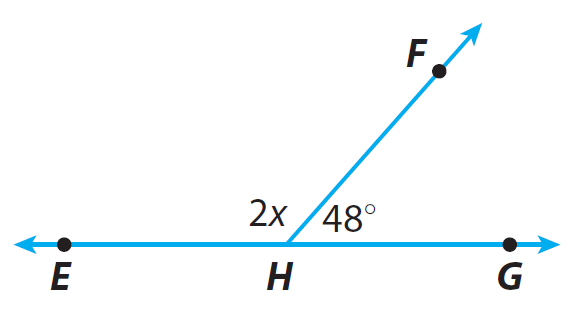
Find the measure of ∠EHF. 

Problem 2 : 

Find the measure of ∠ZXY.

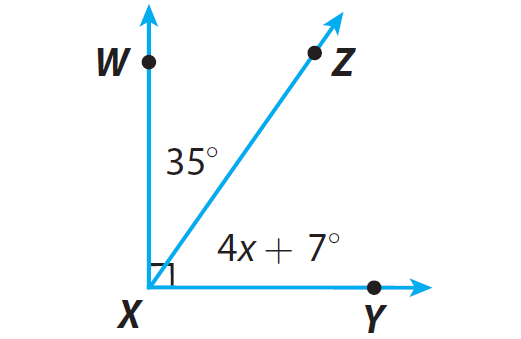
Problem 3 : 

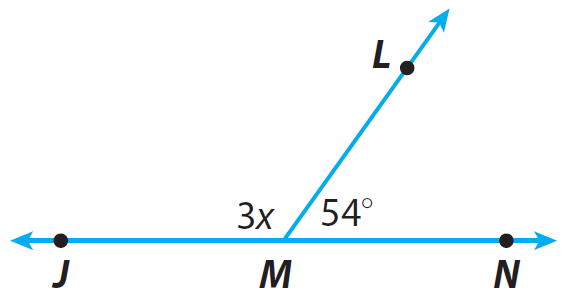
Find the measure of ∠JML.

Detailed Answer Key

Problem 1 :

Find the measure of m∠EHF. 

Step 1 : 

Identify the relationship between m∠EHF and m∠FHG.

Since angles m∠EHF and m∠FHG form a straight line, the sum of the measures of the angles is 180°.

m∠EHF and m∠FHG are supplementary angles.

Step 2 : 

Write and solve an equation to find x. 

The sum of the measures of supplementary angles is 180°.

m∠EHF + m∠FHG  =  180°

2x + 48° = 180°

Subtract 48° from each side. 

2x  =  132°

Divide each side by 2. 

x  =  66° 

Step 3 : 

Find the measure of m∠EHF.

m∠EHF  =  2x

m∠EHF  =  2(66°)

m∠EHF  =  132°

So, the measure of m∠EHF is 132°.

Problem 2 : 

Find the measure of m∠ZXY.

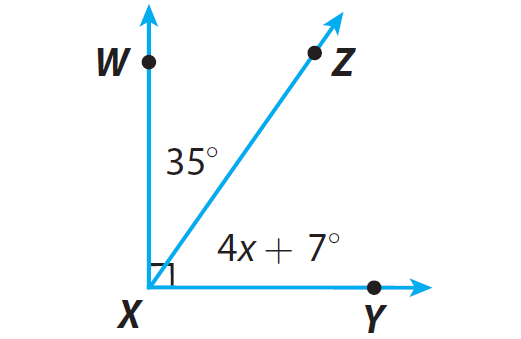
Step 1 : 

Identify the relationship between m∠WXZ and m∠ZXY.

m∠WXZ and m∠ZXY are complementary angles.

Step 2 : 

Write and solve an equation to find x. 

The sum of the measures of complementary angles is 90°.

m∠WXZ + m∠ZXY  =  90°

4x + 7° + 35° = 90°

4x + 42°  =  90°

Subtract 42° from each side. 

4x  =  48°

Divide each side by 4. 

x  =  12° 

Step 3 : 

Find the measure of m∠EHF.

m∠ZXY  =  4x + 7°

m∠ZXY  =  4(12°) + 7°

m∠ZXY  =  48° + 7°

m∠ZXY  =  55°

So, the measure of m∠ZXY is 55°.

Problem 3 : 

Find the measure of m∠JML.

Step 1 : 

Identify the relationship between m∠JML and m∠LMN.

Since angles m∠JML and m∠LMN form a straight line, the sum of the measures of the angles is 180°.

m∠JML and m∠LMN are supplementary angles.

Step 2 : 

Write and solve an equation to find x. 

The sum of the measures of supplementary angles is 180°.

m∠JML + m∠LMN  =  180°

3x + 54° = 180°

Subtract 54° from each side. 

3x  =  126°

Divide each side by 3. 

x  =  42° 

Step 3 : 

Find the measure of m∠JML.

m∠JML  =  3x

m∠JML  =  3(42°)

m∠JML  =  126°

So, the measure of m∠JML is 126°.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.